题目内容
(1)如图(1),已知:在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m,CE⊥直线m,垂足分别为点D、E.证明:DE=BD+CE.
(2)如图(2),将(1)中的条件改为:在△ABC中,AB=AC,D、A、E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC=a,其中a为任意锐角或钝角.请问结论DE=BD+CE是否成立?如成立,请你给出证明;若不成立,请说明理由.
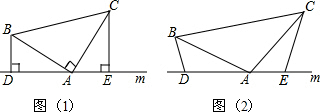
(2)如图(2),将(1)中的条件改为:在△ABC中,AB=AC,D、A、E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC=a,其中a为任意锐角或钝角.请问结论DE=BD+CE是否成立?如成立,请你给出证明;若不成立,请说明理由.

考点:全等三角形的判定与性质
专题:
分析:(1)由条件可证明△ABD≌△CAE,可得DA=CE,AE=BD,可得DE=BD+CE;
(2)由条件可知∠BAD+∠CAE=180°-α,且∠DBA+∠BAD=180°-α,可得∠DBA=∠CAE,结合条件可证明△ABD≌△CAE,同(1)可得出结论.
(2)由条件可知∠BAD+∠CAE=180°-α,且∠DBA+∠BAD=180°-α,可得∠DBA=∠CAE,结合条件可证明△ABD≌△CAE,同(1)可得出结论.
解答:(1)证明:
∵BD⊥DE,CE⊥DE,
∴∠BDA=∠CEA=90°,
∵∠BAC=90°,
∴∠BAD+∠CAE=∠BAD+∠ABD=90°,
∴∠ABD=∠CAE,
在△ABD和△CAE中
∴△ABD≌△CAE(AAS),
∴BD=AE,CE=DA,
∴DE=AE+DA=BD+CE;
(2)解:成立,证明如下:
∵∠BDA=∠AEC=∠BAC=a,
∴∠BAD+∠CAE=180°-α,且∠DBA+∠BAD=180°-α,
∴∠DBA=∠CAE,
在△ABD和△CAE中
∴△ABD≌△CAE(AAS),
∴BD=AE,CE=DA,
∴DE=AE+DA=BD+CE.
∵BD⊥DE,CE⊥DE,
∴∠BDA=∠CEA=90°,
∵∠BAC=90°,
∴∠BAD+∠CAE=∠BAD+∠ABD=90°,
∴∠ABD=∠CAE,
在△ABD和△CAE中
|
∴△ABD≌△CAE(AAS),
∴BD=AE,CE=DA,
∴DE=AE+DA=BD+CE;
(2)解:成立,证明如下:
∵∠BDA=∠AEC=∠BAC=a,
∴∠BAD+∠CAE=180°-α,且∠DBA+∠BAD=180°-α,
∴∠DBA=∠CAE,
在△ABD和△CAE中
|
∴△ABD≌△CAE(AAS),
∴BD=AE,CE=DA,
∴DE=AE+DA=BD+CE.
点评:本题主要考查全等三角形的判定和性质,由条件证明三角形全等得到BD=AE、CE=AD是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 小芳和小明在手工制作课上各自制作楼梯模型,它们用的材料如图①和图②所示,则它们所用材料的周长( )
小芳和小明在手工制作课上各自制作楼梯模型,它们用的材料如图①和图②所示,则它们所用材料的周长( )| A、一样长 | B、小明的长 |
| C、小芳的长 | D、不能确定 |
下列说法中正确的是( )
| A、0是最小的数 |
| B、任何有理数的绝对值都是正数 |
| C、如果两个数互为相反数,那么它们的绝对值相等 |
| D、最大的负有理数是-1 |
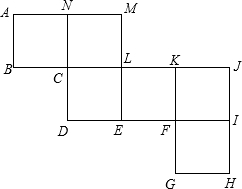 把如图的纸片折叠成一个正方形.
把如图的纸片折叠成一个正方形.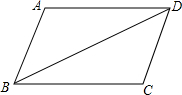 如图,已知:∠ABC=∠ADC,AD∥BC.
如图,已知:∠ABC=∠ADC,AD∥BC.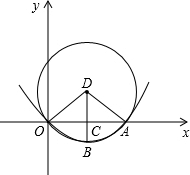 ⊙O经过坐标原点,且与x轴交于点A、DC⊥x轴于点C,且与⊙D交于点B,已知⊙D的半径为2
⊙O经过坐标原点,且与x轴交于点A、DC⊥x轴于点C,且与⊙D交于点B,已知⊙D的半径为2