题目内容
19.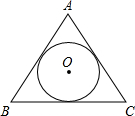 如图,若等边△ABC的内切圆⊙O的半径是2,则△ABC的面积是( )
如图,若等边△ABC的内切圆⊙O的半径是2,则△ABC的面积是( )| A. | 4$\sqrt{3}$ | B. | 6$\sqrt{3}$ | C. | 8$\sqrt{3}$ | D. | 12$\sqrt{3}$ |
分析 连接OB,OD,根据⊙O是等边△ABC的内切圆,求出∠OBD=30°,求出OB=2OD=4,根据勾股定理求出BD,同理求出CD,得到BC,求出AD,即可得出答案.
解答  解:连接OB,OD,OA,
解:连接OB,OD,OA,
∵⊙O是等边△ABC的内切圆,
∴∠OBD=30°,∠BDO=90°,
∴OB=2OD=4,
由勾股定理得:BD=$\sqrt{{OB}^{2}{-OD}^{2}}$=2$\sqrt{3}$,
同理CD=2$\sqrt{3}$,
∴BC=BD+CD=4$\sqrt{3}$,
∵△ABC是等边三角形,A,O,D三点共线,
∴AD=6,
∴S△ABC=$\frac{1}{2}$BC•AD=12$\sqrt{3}$.
点评 本题考查了等边三角形性质,三角形的内切圆,勾股定理,含30度角的直角三角形性质等知识点的应用,关键是构造直角三角形,并求出OB和BD的长,题目较好,难度适中.

练习册系列答案
相关题目
7.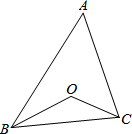 如图,在△ABC中,∠A=50°,点O是它的内心,则∠BOC等于( )
如图,在△ABC中,∠A=50°,点O是它的内心,则∠BOC等于( )
 如图,在△ABC中,∠A=50°,点O是它的内心,则∠BOC等于( )
如图,在△ABC中,∠A=50°,点O是它的内心,则∠BOC等于( )| A. | 125° | B. | 115° | C. | 105° | D. | 95° |
8.若圆锥的母线长是底面半径的3倍,则将圆锥的侧面展开后的扇形的圆心角是( )
| A. | 60° | B. | 90° | C. | 120° | D. | 150° |
9.下列命题的逆命题是假命题的是( )
| A. | 如果两个数的绝对值相等,那么这两个数相等 | |
| B. | 两直线平行,内错角相等 | |
| C. | 矩形的四个角都相等 | |
| D. | 对顶角相等 |
 已知:如图,AD∥BC,∠ABD=∠D.求证:BD平分∠ABC.
已知:如图,AD∥BC,∠ABD=∠D.求证:BD平分∠ABC.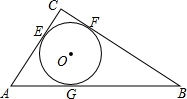 在Rt△ABC中,∠C=90°,AC=3,BC=4,AB=5.如图,⊙O是△ABC的内切圆,与三边分别相切于点E、F、G.
在Rt△ABC中,∠C=90°,AC=3,BC=4,AB=5.如图,⊙O是△ABC的内切圆,与三边分别相切于点E、F、G.