题目内容
10. 已知:如图,AD∥BC,∠ABD=∠D.求证:BD平分∠ABC.
已知:如图,AD∥BC,∠ABD=∠D.求证:BD平分∠ABC.
分析 先利用平行线的性质得到∠D=∠CBD,加上∠ABD=∠D,则利用等量代换得到∠ABD=∠CBD,于是可判断BD平分∠ABC.
解答 证明:∵AD∥BC,
∴∠D=∠CBD,
∵∠ABD=∠D,
∴∠ABD=∠CBD,
∴BD平分∠ABC.
点评 本题考查了平行线性质:两直线平行,同位角相等;两直线平行,同旁内角互补;两直线平行,内错角相等.

练习册系列答案
 巧学巧练系列答案
巧学巧练系列答案
相关题目
19.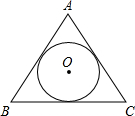 如图,若等边△ABC的内切圆⊙O的半径是2,则△ABC的面积是( )
如图,若等边△ABC的内切圆⊙O的半径是2,则△ABC的面积是( )
 如图,若等边△ABC的内切圆⊙O的半径是2,则△ABC的面积是( )
如图,若等边△ABC的内切圆⊙O的半径是2,则△ABC的面积是( )| A. | 4$\sqrt{3}$ | B. | 6$\sqrt{3}$ | C. | 8$\sqrt{3}$ | D. | 12$\sqrt{3}$ |
20.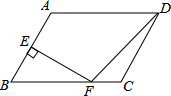 在?ABCD中,AB=6,AD=8,∠ABC=60°,点E是AB的中点,EF⊥AB交BC于F,连接DF,则DF的长为( )
在?ABCD中,AB=6,AD=8,∠ABC=60°,点E是AB的中点,EF⊥AB交BC于F,连接DF,则DF的长为( )
 在?ABCD中,AB=6,AD=8,∠ABC=60°,点E是AB的中点,EF⊥AB交BC于F,连接DF,则DF的长为( )
在?ABCD中,AB=6,AD=8,∠ABC=60°,点E是AB的中点,EF⊥AB交BC于F,连接DF,则DF的长为( )| A. | 2$\sqrt{13}$ | B. | 8 | C. | 5$\sqrt{2}$ | D. | 10 |
 如图,已知梯形ABCD中,AD∥BC,∠A=90°,AD=AB=1cm,CD=$\sqrt{3}$cm,求梯形ABCD的面积.
如图,已知梯形ABCD中,AD∥BC,∠A=90°,AD=AB=1cm,CD=$\sqrt{3}$cm,求梯形ABCD的面积.
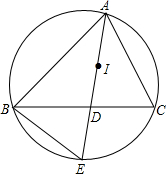 如图,I是△ABC的内心,AI的延长线交边BC于点D,交△ABC的外接圆于点E.
如图,I是△ABC的内心,AI的延长线交边BC于点D,交△ABC的外接圆于点E.