题目内容
7.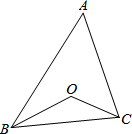 如图,在△ABC中,∠A=50°,点O是它的内心,则∠BOC等于( )
如图,在△ABC中,∠A=50°,点O是它的内心,则∠BOC等于( )| A. | 125° | B. | 115° | C. | 105° | D. | 95° |
分析 利用三角形的内心的性质得出∠ABO+∠ACO=∠OBC+∠OCB=65°,进而得出答案.
解答 解:∵点O是△ABC的内心,
∴∠ABO=∠OBC,∠ACO=∠OCB,
∵∠A=50°,
∴∠ABC+∠ACB=130°,
∴∠ABO+∠ACO=∠OBC+∠OCB=65°,
则∠BOC=180°-65°=115°.
故选B.
点评 此题主要考查了三角形内心的性质以及三角形内角和定理,根据已知得出∠ABO+∠ACO=∠OBC+∠OCB=65°是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
19.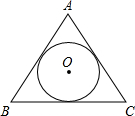 如图,若等边△ABC的内切圆⊙O的半径是2,则△ABC的面积是( )
如图,若等边△ABC的内切圆⊙O的半径是2,则△ABC的面积是( )
 如图,若等边△ABC的内切圆⊙O的半径是2,则△ABC的面积是( )
如图,若等边△ABC的内切圆⊙O的半径是2,则△ABC的面积是( )| A. | 4$\sqrt{3}$ | B. | 6$\sqrt{3}$ | C. | 8$\sqrt{3}$ | D. | 12$\sqrt{3}$ |
17.下列条件中,不能判断△ABC为直角三角形的是( )
| A. | a2=1,b2=2,c2=3 | B. | a:b:c=3:4:5 | C. | ∠A+∠B=∠C | D. | ∠A:∠B:∠C=3:4:5 |
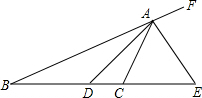 如图,AD是△ABC中∠BAC的平分线,AE是△ABC的外角平分线,AE交BC的延长线于点E,∠BAD=20°,∠E=50°,求∠ACD的度数.
如图,AD是△ABC中∠BAC的平分线,AE是△ABC的外角平分线,AE交BC的延长线于点E,∠BAD=20°,∠E=50°,求∠ACD的度数.
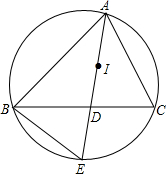 如图,I是△ABC的内心,AI的延长线交边BC于点D,交△ABC的外接圆于点E.
如图,I是△ABC的内心,AI的延长线交边BC于点D,交△ABC的外接圆于点E. 如图,⊙O与△ABC各边切于点D、E、F,且∠C=60°,∠EOF=100°,求∠B的度数.
如图,⊙O与△ABC各边切于点D、E、F,且∠C=60°,∠EOF=100°,求∠B的度数.