题目内容
15.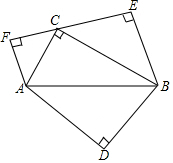 如图,在Rt△ABC中,∠ACB=90°,AC=1,BC=2,分别以三条边为斜边作等腰直角三角形ABD,BCE,ACF,则四边形ADBC的面积是$\frac{9}{5}$.
如图,在Rt△ABC中,∠ACB=90°,AC=1,BC=2,分别以三条边为斜边作等腰直角三角形ABD,BCE,ACF,则四边形ADBC的面积是$\frac{9}{5}$.
分析 根据四边形ADBC的面积=S△ABC+S△ABD计算即可.
解答 解:在Rt △ABC中,∵AC=1,BC=2,
△ABC中,∵AC=1,BC=2,
∴AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=$\sqrt{5}$,
∵AD=BD,∠D=90°,
∴AD=BD=$\frac{\sqrt{10}}{2}$,
∴四边形ADBC的面积=S△ABC+S△ABD=$\frac{1}{2}$×1×2+$\frac{1}{2}$×$\frac{\sqrt{10}}{2}$×$\frac{\sqrt{10}}{2}$=$\frac{9}{5}$.
故答案为$\frac{9}{5}$.
点评 本题考查勾股定理、等腰直角三角形的性质、四边形的面积等知识,解题的关键是把四边形问题转化为三角形问题解决,属于中考常考题型.

练习册系列答案
相关题目
5.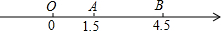 如图,点O、A、B在数轴上,分别表示数0、1.5、4.5,数轴上另有一点C,到点A的距离为1,到点B的距离小于3,则点C位于( )
如图,点O、A、B在数轴上,分别表示数0、1.5、4.5,数轴上另有一点C,到点A的距离为1,到点B的距离小于3,则点C位于( )
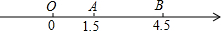 如图,点O、A、B在数轴上,分别表示数0、1.5、4.5,数轴上另有一点C,到点A的距离为1,到点B的距离小于3,则点C位于( )
如图,点O、A、B在数轴上,分别表示数0、1.5、4.5,数轴上另有一点C,到点A的距离为1,到点B的距离小于3,则点C位于( )| A. | 点O的左边 | B. | 点O与点A之间 | C. | 点B的右边 | D. | 点A与点B之间 |