题目内容
18.在$\sqrt{4}$,0.333…,$\frac{22}{7}$,0.3030030003…,π,$\root{3}{9}$,0中,有理数的个数为( )| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
分析 根据有理数是整数、有限小数或无限循环小数,可得答案.
解答 解:在$\sqrt{4}$=2,0.333…,$\frac{22}{7}$,0.3030030003…,π,$\root{3}{9}$,0中,有理数有$\sqrt{4}$,0.333…,$\frac{22}{7}$,0,有理数的个数为4.
故选:B.
点评 本题考查了实数,关键是熟悉有理数是整数、有限小数或无限循环小数的知识点.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
9.如果a>b,则下列不等式中成立的是( )
| A. | a-3<b-3 | B. | 3-a<3-b | C. | $\frac{1}{3}$a<$\frac{1}{3}$b | D. | -2a>-2b |
6.若x2+2xy+y2=(x-y)2-A,则A为( )
| A. | 2xy | B. | -2xy | C. | -4xy | D. | 4xy |
7.方程(y+1)(y-1)=2y2-4y-6化为一般形式为( )
| A. | y2-4y+5=0 | B. | y2-4y-5=0 | C. | y2+4y-5=0 | D. | y2+4y+5=0 |
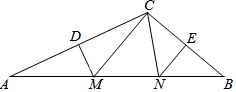 如图,在△ABC中,DM、EN分别垂直平分AC和BC,交AB于M、N,
如图,在△ABC中,DM、EN分别垂直平分AC和BC,交AB于M、N,