题目内容
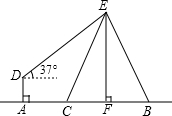 如图,在电线杆上的E处引拉线EC和EB固定电线杆,在离电线杆6米的A处安置测角仪(点A,C,F在一直线上),在D处测得电线杆上E处的仰角为37°,已知测角仪的高AD为1.5米,AC为3米,求拉线EC的长.(精确到0.1米)
如图,在电线杆上的E处引拉线EC和EB固定电线杆,在离电线杆6米的A处安置测角仪(点A,C,F在一直线上),在D处测得电线杆上E处的仰角为37°,已知测角仪的高AD为1.5米,AC为3米,求拉线EC的长.(精确到0.1米)考点:解直角三角形的应用-仰角俯角问题
专题:
分析:由题意可先过点D作DM⊥EF,垂足为M,在Rt△EMD中,可求出EM,进而EF=EM+MF,再在Rt△CEF中,求出CE的长.
解答: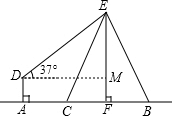 解:过点D作DM⊥EF,垂足为M,
解:过点D作DM⊥EF,垂足为M,
由题意可知四边形ADMF为矩形,
∴DM=AF=6,MF=DA=1.5,
在Rt△EMD中,EM=DM•tan∠EDM=6tan37°,
∴EF=EM+MF,DM=AF=6tan37°,
∴EF=EM+MF=6tan37°+1.5.
∵AC=3,
∴CF=AF-AC=3,
在Rt△CEF中,CE=
≈6.7.
答:拉线CE的长为6.7米.
 解:过点D作DM⊥EF,垂足为M,
解:过点D作DM⊥EF,垂足为M,由题意可知四边形ADMF为矩形,
∴DM=AF=6,MF=DA=1.5,
在Rt△EMD中,EM=DM•tan∠EDM=6tan37°,
∴EF=EM+MF,DM=AF=6tan37°,
∴EF=EM+MF=6tan37°+1.5.
∵AC=3,
∴CF=AF-AC=3,
在Rt△CEF中,CE=
| CF2+EF2 |
答:拉线CE的长为6.7米.
点评:此题主要考查解直角三角形的应用.要求学生借助仰角关系构造直角三角形,并结合图形利用三角函数解直角三角形.

练习册系列答案
相关题目
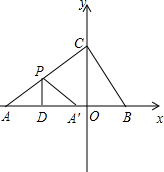 Rt△ABC中,∠ACB=90°,∠CAB=30°,点A、B、C在坐标轴上,点C的坐标为(0,2),点D在射线AB上运动,过点D作PD⊥AB,交直线AC于点P,作过点A关于PD的对称点A′,连接PA′,点D的运动速度为每秒
Rt△ABC中,∠ACB=90°,∠CAB=30°,点A、B、C在坐标轴上,点C的坐标为(0,2),点D在射线AB上运动,过点D作PD⊥AB,交直线AC于点P,作过点A关于PD的对称点A′,连接PA′,点D的运动速度为每秒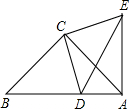 如图,△ABC与△CDE都是等腰直角三角形,∠ACB=∠DCE=90°,DB=4,AB=7,求DE的长.
如图,△ABC与△CDE都是等腰直角三角形,∠ACB=∠DCE=90°,DB=4,AB=7,求DE的长. 如图,矩形ABCD中,对角线AC、BD相交于点O,AC=6,则OD=
如图,矩形ABCD中,对角线AC、BD相交于点O,AC=6,则OD=