题目内容
已知三点A(0,3),B(-1,0),C(3,0),试求点D的坐标,使这四点成为等腰梯形的顶点.
考点:等腰梯形的性质,坐标与图形性质
专题:
分析:根据等腰梯形的性质,分三种情况构造等腰梯形求解即可.
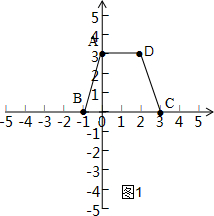
解答:解:①如图1,过A作BC的平行线,AB=CD可得等腰梯形,
∵A(0,3),B(-1,0),C(3,0),
∴AB=
=
,
∵AD∥BC,
∴D的纵坐标为3,故横坐标为3-1=2时AB=CD,
∴点D(2,3).
②如图2,过C作AB的平行线,AD=BC可得等腰梯形,作DF⊥x轴交x轴于点F,设点D(x,y),
∵
=3,
∴
=3,即
=3,
∵x2+y2═16,联立解得
,
(舍去).
∴点D(
,
).
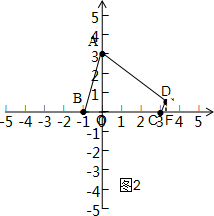
③如图3,过B作AC的平行线,AB=CD可得等腰梯形,
∵A(0,3),B(-1,0),C(3,0),
∴AB=
=
,
∵BD∥AC,
∴BD过-1,当点D在-1处时有CD=
=
,
∴点D(0,-1).
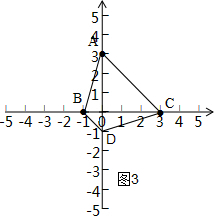
综上所述,点D的坐标为(2,3),(
,
)或(0,-1).
∵A(0,3),B(-1,0),C(3,0),
∴AB=
| 12+33 |
| 10 |
∵AD∥BC,
∴D的纵坐标为3,故横坐标为3-1=2时AB=CD,
∴点D(2,3).

②如图2,过C作AB的平行线,AD=BC可得等腰梯形,作DF⊥x轴交x轴于点F,设点D(x,y),
∵
| AO |
| BO |
∴
| DF |
| CF |
| y |
| x-3 |
∵x2+y2═16,联立解得
|
|
∴点D(
| 16 |
| 5 |
| 3 |
| 5 |
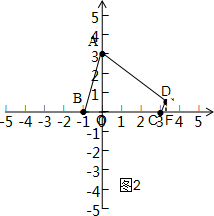
③如图3,过B作AC的平行线,AB=CD可得等腰梯形,
∵A(0,3),B(-1,0),C(3,0),
∴AB=
| 12+33 |
| 10 |
∵BD∥AC,
∴BD过-1,当点D在-1处时有CD=
| 12+33 |
| 10 |
∴点D(0,-1).
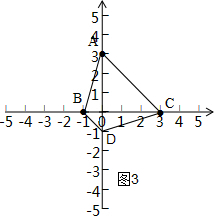
综上所述,点D的坐标为(2,3),(
| 16 |
| 5 |
| 3 |
| 5 |
点评:本题主要考查了等腰梯形的性质及坐标与图形性质,解题的关键是根据两底平行,两腰相等构造等腰梯形.

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案
相关题目
 已知梯形ABCD中,AD∥BC,E、F分别在AB、CD上,求证:若ED∥BF,则AF∥CE.
已知梯形ABCD中,AD∥BC,E、F分别在AB、CD上,求证:若ED∥BF,则AF∥CE.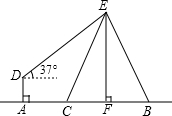 如图,在电线杆上的E处引拉线EC和EB固定电线杆,在离电线杆6米的A处安置测角仪(点A,C,F在一直线上),在D处测得电线杆上E处的仰角为37°,已知测角仪的高AD为1.5米,AC为3米,求拉线EC的长.(精确到0.1米)
如图,在电线杆上的E处引拉线EC和EB固定电线杆,在离电线杆6米的A处安置测角仪(点A,C,F在一直线上),在D处测得电线杆上E处的仰角为37°,已知测角仪的高AD为1.5米,AC为3米,求拉线EC的长.(精确到0.1米) 如图,反比例函数y=
如图,反比例函数y=