题目内容
9.与x轴无交点的抛物线是( )| A. | y=2x2-3 | B. | y=x2+2x | C. | y=-$\frac{1}{3}$(x-1)2-1 | D. | y=-$\frac{1}{3}$x2+1 |
分析 根据△=b2-4ac决定抛物线与x轴的交点个数,通过计算A、B、D选项中的判别式的值可对A、B、D进行判断;根据二次函数的性质可对C进行判断.
解答 解:A、△=02-4×2×(-3)>0,则抛物线与x轴有2个交点,所以A选项错误;
B、△=22-4×1×0>0,则抛物线与x轴有2个交点,所以B选项错误;
C、y≤-1,而抛物线开口向下,则抛物线与x轴没有交点,所以C选项正确;
D、△=02-4×(-$\frac{1}{3}$)×1>0,则抛物线与x轴有2个交点,所以D选项错误.
故选C.
点评 本题考查了抛物线与x轴的交点:把求二次函数y=ax2+bx+c(a,b,c是常数,a≠0)与x轴的交点坐标问题可转化为解关于x的一元二次方程.对于二次函数y=ax2+bx+c(a,b,c是常数,a≠0),△=b2-4ac决定抛物线与x轴的交点个数.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案
相关题目
 某城区规划局为了方便居民的生活,计划在三个住宅小区A,B,C(如图所示) 之间建购物商场,该购物商场建在何处才能使这三个住宅小区的居民到该购物商场距离相等?
某城区规划局为了方便居民的生活,计划在三个住宅小区A,B,C(如图所示) 之间建购物商场,该购物商场建在何处才能使这三个住宅小区的居民到该购物商场距离相等?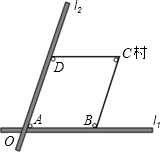 如图,两条笔直的公路l1、l2相交于点O,村庄C的村民在公路的旁边建三个加工厂A、B、D.已知AB=BC=CD=DA=5公里,村庄C到公路l1的距离为4公里,则村庄C到公路l2的距离是( )
如图,两条笔直的公路l1、l2相交于点O,村庄C的村民在公路的旁边建三个加工厂A、B、D.已知AB=BC=CD=DA=5公里,村庄C到公路l1的距离为4公里,则村庄C到公路l2的距离是( ) 如图,六边形在正方形网格内,连接六边形中两两不相邻的三个顶点,得到△AEC,说明为什么这个三角形的面积等于六边形面积的一半.
如图,六边形在正方形网格内,连接六边形中两两不相邻的三个顶点,得到△AEC,说明为什么这个三角形的面积等于六边形面积的一半.