题目内容
18. 如图,六边形在正方形网格内,连接六边形中两两不相邻的三个顶点,得到△AEC,说明为什么这个三角形的面积等于六边形面积的一半.
如图,六边形在正方形网格内,连接六边形中两两不相邻的三个顶点,得到△AEC,说明为什么这个三角形的面积等于六边形面积的一半.
分析 首先利用长方形的面积减去四个直角三角形的面积得出六边形的面积,进一步计算△ABC、△AFE、△CDE的面积和,得出△AEC的面积与六边形的面积比较得出答案即可.
解答 解:六边形的面积=8×5-$\frac{1}{2}$×2×1×2-$\frac{1}{2}$×3×2×2=40-2-6=32;
△ABC、△AFE、△CDE的面积和为$\frac{1}{2}$×(1+2)×5-$\frac{1}{2}$×2×1-$\frac{1}{2}$×3×2+$\frac{1}{2}$×5×3+$\frac{1}{2}$×5×2=7.5-1-3+7.5+5=16,
则△AEC的面积=32-16=16,
也就是△AEC的面积等于六边形面积的一半.
点评 此题考查三角形的面积,把不规则图形分成基本平面图形,利用面积计算公式求得面积,此题关键是求得△ABC的面积.

练习册系列答案
相关题目
8.估算$\sqrt{37}$-3(误差小于1)的大小是( )
| A. | 6 | B. | 3 | C. | 3或4 | D. | 4或5 |
9.与x轴无交点的抛物线是( )
| A. | y=2x2-3 | B. | y=x2+2x | C. | y=-$\frac{1}{3}$(x-1)2-1 | D. | y=-$\frac{1}{3}$x2+1 |
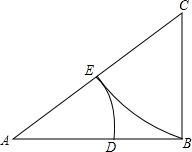 已知小强将线段AB黄金分割(点D为黄金分割点)所作的图形如图所示.请你回答:
已知小强将线段AB黄金分割(点D为黄金分割点)所作的图形如图所示.请你回答: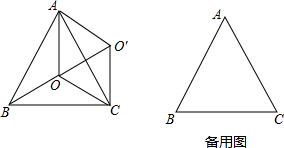
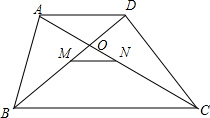 如图,在四边形ABCD中,AD∥BC,AD<BC,M,N分别是对角线BD,AC的中点,试探索MN与两底的位置关系与数量关系,并说明理由.
如图,在四边形ABCD中,AD∥BC,AD<BC,M,N分别是对角线BD,AC的中点,试探索MN与两底的位置关系与数量关系,并说明理由.