题目内容
20．在平面直角坐标系中，抛物线y=ax2+bx+c与x轴交于A（3，0），B（-2，0）两点，与y轴交于C（0，-6），将其向上（下）或向左（右）平移m（m＞0）个单位长度，使平移后的抛物线恰好经过原点，则m的最小值为2．分析 根据函数图象所经过的点A、B、C作出大致图象，结合图象直接回答问题．
解答 解：∵抛物线y=ax2+bx+c与x轴交于A（3，0），B（-2，0）两点，与y轴交于C（0，-6），
∴其大致图象如图所示：
．
由图示知，当抛物线y=ax2+bx+c向上平移6个单位或向右平移2个单位或向左平移3个单位后，平移后的抛物线恰好经过原点，
即m=6或m=2或m=3，
所以m的最小值为2．
故答案是：2．
点评 本题考查了二次函数图象与几何变换．解答该题的关键是根据抛物线与坐标轴的交点坐标画出二次函数的大致图象，解题时，利用了“数形结合”是数学思想，使问题变得直观化，降低了题的难度．
练习册系列答案
习题精选系列答案
相关题目
8．估算$\sqrt{37}$-3（误差小于1）的大小是（ ）
| A． | 6 | B． | 3 | C． | 3或4 | D． | 4或5 |
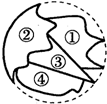一圆形玻璃被打碎后，其中四块碎片如图所示，若选择其中一块碎片带到商店，配制与原来大小一样的圆形玻璃，选择的是（ ）
9．与x轴无交点的抛物线是（ ）
| A． | y=2x2-3 | B． | y=x2+2x | C． | y=-$\frac{1}{3}$（x-1）2-1 | D． | y=-$\frac{1}{3}$x2+1 |
