题目内容
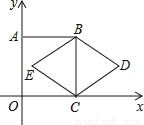
如图,在正方形ABCD中,E是AB上一点,F是AD延长线上一点,且DF=BE.
(1)求证:CE=CF;
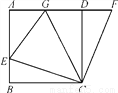
(2)若点G在AD上,且∠GCE=45°,则GE=BE+GD成立吗?为什么?
(1)证明见解析(2)GE=BE+GD成立 【解析】试题分析:(1)由DF=BE,四边形ABCD为正方形可证△CEB≌△CFD,从而证出CE=CF; (2)由(1)得CE=CF,∠BCE+∠ECD=∠DCF+∠ECD,即∠ECF=∠BCD=90°,又∠GCE=45°,所以可得∠GCE=∠GCF,故可证得△ECG≌△FCG,即EG=FG=GD+DF.又因为DF=BE,所以可证出GE=BE...
练习册系列答案
相关题目
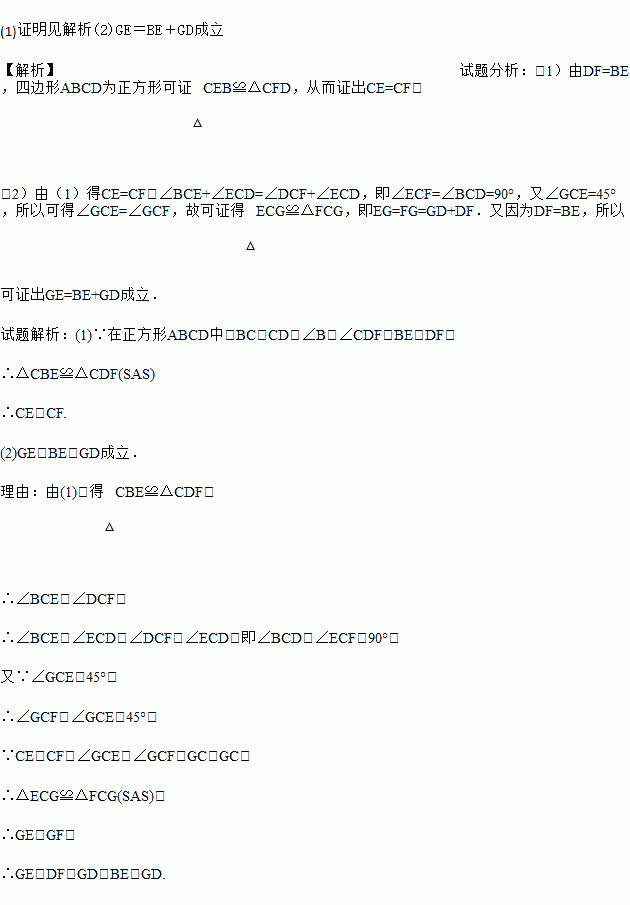

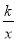 的图象与一次函数y=kx+m的图象相交于点A(2,1).
的图象与一次函数y=kx+m的图象相交于点A(2,1).
 .
.
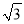 )2-|-6|+(-2)0; (2) (2x+1)(2x-1)-4(x+1)2.
)2-|-6|+(-2)0; (2) (2x+1)(2x-1)-4(x+1)2. B.
B.  C.
C.  D.
D. 