题目内容
16．
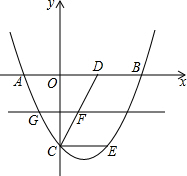如图，抛物线y=$\frac{1}{2}$x2-x-4过平行四边形CEBD的三点，过DC中点F作直线m平行x轴，交抛物线左侧于点G．（1）G点坐标；
（2）x轴上一点P，使得G，F，D，P能成为平行四边形，求P点坐标．
分析 （1）首先确定点G的纵坐标，代入抛物线求出横坐标，继而可得点G的坐标；
（2）求出FG的长度，分两种情况：①当GD为边时，求出点P的坐标；②当GD是对角线时，求出P点坐标．
解答 解：（1）将y=-2代入y=$\frac{1}{2}$x2-x-4中，
解得：x=1±$\sqrt{5}$，
则G点坐标为：（1-$\sqrt{5}$，-2）．
（2）∵C（0，-4），D（2，0），F为DC中点，
∴F（1，-2），
∵G（1-$\sqrt{5}$，-2），
∴FG=$\sqrt{5}$，
∵G，F，D，P为平行四边形，
∴GF∥DP且GF=DP，
当GD是边时，P1（2-$\sqrt{5}$，0）；
当GD是对角线时，P2（2+$\sqrt{5}$，0）；
综上可得：使得G，F，D，P能成为平行四边形的P点坐标为（2-$\sqrt{5}$，0）或（2+$\sqrt{5}$，0）．
点评 本题考查了二次函数的综合，难点在第二问，解题的关键是分类讨论，避免漏解，注意数形结合思想的应用，难度一般．
练习册系列答案
相关题目
（1）计算：（a+3b）（a-3b）+（a-3b）2-2a2；
4．
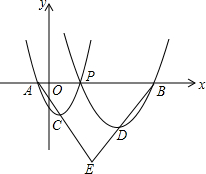如图，已知点A（-1，0），B（7，0），P是线段AB上任意一点（不含端点A，B），过A、P两点的二次函数y1和过P、B两点的二次函数y2的图象开口均向上，它们的顶点分别为C、D，射线BD与AC相交于点E．当AE=BE=5时，这两个二次函数的最小值之和等于（ ）
如图，已知点A（-1，0），B（7，0），P是线段AB上任意一点（不含端点A，B），过A、P两点的二次函数y1和过P、B两点的二次函数y2的图象开口均向上，它们的顶点分别为C、D，射线BD与AC相交于点E．当AE=BE=5时，这两个二次函数的最小值之和等于（ ）| A． | -1 | B． | -2 | C． | -3 | D． | -4 |
如图，点A、B、C在直线l上，点P在直线l外，PB⊥l于点B，则点P到直线l的距离是线段PB的长度．
8．
如图，Rt△ABC中，∠C=90°，∠ABC的平分线BD交AC于D．若AB=m，CD=n，则△ABD的面积等于（ ）
如图，Rt△ABC中，∠C=90°，∠ABC的平分线BD交AC于D．若AB=m，CD=n，则△ABD的面积等于（ ）| A． | mn | B． | $\frac{1}{2}mn$ | C． | 2mn | D． | $\frac{1}{3}mn$ |
如图，射线OA的方向是北偏西60°，射线OB的方向是南偏东25°，则∠AOB=145°．