题目内容
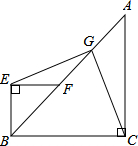 已知,如图,在△ABC中,∠ACB=90°,AC=BC,等腰直角三角形BEF的斜边在AB上,点G是AF的中点,联结EG,CG,求证:EG⊥CG.
已知,如图,在△ABC中,∠ACB=90°,AC=BC,等腰直角三角形BEF的斜边在AB上,点G是AF的中点,联结EG,CG,求证:EG⊥CG.考点:全等三角形的判定与性质
专题:证明题
分析:作GH⊥AB,垂直是G,根据勾股定理证明EF=CH,然后证明△GEF≌△GCH,根据全等三角形的对应边相等即可证得∠EGF=∠CGH,进而证明垂直关系.
解答:
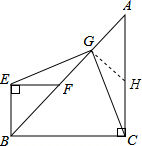 证明:作GH⊥AB,垂直是G.
证明:作GH⊥AB,垂直是G.
则△AGH是等腰直角三角形,
∴AG=GH,
设AC=CB=a,BE=EF=b.
由勾股定理可得:AB=
a,BF=
b.
又∵点G是AF的中点,
∴GF=GH=AG=
(a-b).
在直角△AGH中,AH=a-b,
∴CH=AC-AH=a-(a-b)=b,又EF=b,
∴GF=CH,∠GFE=135°,∠GHC=135°,
在△EGF和△GCH中,
∴△GEF≌△GCH(SAS),
∴∠EGF=∠CGH,
∴∠EGC=∠EGF+∠FGC=∠CGH+∠FGC=90°,
∴EG⊥CG.
 证明:作GH⊥AB,垂直是G.
证明:作GH⊥AB,垂直是G.则△AGH是等腰直角三角形,
∴AG=GH,
设AC=CB=a,BE=EF=b.
由勾股定理可得:AB=
| 2 |
| 2 |
又∵点G是AF的中点,
∴GF=GH=AG=
| ||
| 2 |
在直角△AGH中,AH=a-b,
∴CH=AC-AH=a-(a-b)=b,又EF=b,
∴GF=CH,∠GFE=135°,∠GHC=135°,
在△EGF和△GCH中,
|
∴△GEF≌△GCH(SAS),
∴∠EGF=∠CGH,
∴∠EGC=∠EGF+∠FGC=∠CGH+∠FGC=90°,
∴EG⊥CG.
点评:本题考查了全等三角形的判定与性质以及勾股定理,正确作出辅助线,构造全等的三角形是关键.

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目
 如图,一个直角三角形ABC的斜边AB与量角器的零刻度线重合,点D对应56°,则∠BCD的度数为( )
如图,一个直角三角形ABC的斜边AB与量角器的零刻度线重合,点D对应56°,则∠BCD的度数为( )| A、28° | B、56° |
| C、62° | D、64° |
 如图,点B、E、C、F在同一直线上,AB=DE,AC=DF,BE=CF.求证:CA=CD.
如图,点B、E、C、F在同一直线上,AB=DE,AC=DF,BE=CF.求证:CA=CD. 如图,△ABC的边AB是⊙O的直径,⊙O与AC交于点D,∠BOD=90°,∠B=60°,则∠C=
如图,△ABC的边AB是⊙O的直径,⊙O与AC交于点D,∠BOD=90°,∠B=60°,则∠C=