题目内容
11.先化简($\frac{3}{x+1}$-x+1)÷$\frac{{x}^{2}-4x+4}{x+1}$,再求值,其中x=2-$\sqrt{2}$.分析 先根据分式混合运算的法则把原式进行化简,再把x的值代入进行计算即可.
解答 解:原式=$\frac{-(x+2)(x-2)}{x+1}$•$\frac{x+1}{(x-2)^{2}}$
=$\frac{x+2}{2-x}$,
当x=2-$\sqrt{2}$时,原式=$\frac{2-\sqrt{2}+2}{2-2+\sqrt{2}}$=$\frac{4-\sqrt{2}}{\sqrt{2}}$=2$\sqrt{2}$-1.
点评 本题考查的是分式的化简求值,熟知分式混合运算的法则是解答此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
2.x与3的和的一半是正数,用不等式表示为( )
| A. | $\frac{1}{2}$x+3>0 | B. | $\frac{1}{2}$x+3<0 | C. | $\frac{1}{2}$(x+3)>0 | D. | $\frac{1}{2}$(x+3)<0 |
3.关于x的一元一次不等式(m-1)x>4的解集是x<-1,则( )
| A. | m<0 | B. | m>-3 | C. | m<-3 | D. | m=-3 |
1.圆锥的底面半径为5cm,侧面积为65πcm2,则圆锥的高的长度为( )
| A. | 11cm | B. | 12cm | C. | 13 cm | D. | 14cm |
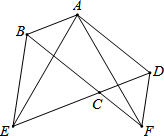 如图,在?ABCD中,∠BCD=120°,分别延长DC、BC到点E,F,使得△BCE和△CDF都是正三角形.
如图,在?ABCD中,∠BCD=120°,分别延长DC、BC到点E,F,使得△BCE和△CDF都是正三角形. 如图,在平面直角坐标系中,Rt△ABC的三个顶点分别是A(-4,2)、B(0,4)、C(0,2),
如图,在平面直角坐标系中,Rt△ABC的三个顶点分别是A(-4,2)、B(0,4)、C(0,2),