题目内容
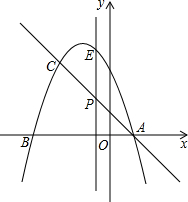 如图,抛物线y=-x2-2x+3与x轴交A、B两点(A点在B点右侧),直线l与抛物线交于A、C两点,其中C点的横坐标为-2.
如图,抛物线y=-x2-2x+3与x轴交A、B两点(A点在B点右侧),直线l与抛物线交于A、C两点,其中C点的横坐标为-2.(1)求A、B两点的坐标及直线AC的函数表达式;
(2)若点P是线段AC上的一个动点,过P点作y轴的平行线交抛物线于E点,求当点P坐标为多少时,线段PE长度有最大值,最大值是多少?
(3)点G是抛物线上的动点,在x轴上是否存在点F,使A、C、F、G这样的四个点为顶点的四边形是平行四边形?如果存在,求出所有满足条件的F点坐标;如果不存在,请说明理由.
考点:二次函数综合题
专题:
分析:(1)先根据C点的横坐标求得纵坐标,然后将A、C的坐标代入抛物线的解析式中,即可求得待定系数的值.
(2)根据抛物线的解析式和直线的解析式,设出P、E的坐标,根据题意列出PE=-m2-2m+3-(-m+1)=-m2-m+2=-(m+
)2+
,即可求得.
(3)此题可分作两种情况考虑:
①CE∥DG;根据抛物线的解析式可求得D点坐标,可得C、D关于抛物线对称轴对称,即C、D的纵坐标相同,所以CD∥x轴,那么C点就是符合条件的G点,易求得CD的长,根据平行四边形的性质知AE=CD,由此可得到AE的长,将A点坐标向左或向右平移CD个单位即可得到两个符合条件的E点坐标;
②AC∥EG;根据平行四边形的性质知,此时G、C的纵坐标互为相反数,由此可求得G点的纵坐标,将其代入抛物线的解析式中即可求得G点的坐标;那么将G点的横坐标减去3(A、C横坐标差的绝对值),即可得到两个符合条件的E点坐标;
综上所述,符合条件的E点坐标应该有4个.
(2)根据抛物线的解析式和直线的解析式,设出P、E的坐标,根据题意列出PE=-m2-2m+3-(-m+1)=-m2-m+2=-(m+
| 1 |
| 2 |
| 9 |
| 4 |
(3)此题可分作两种情况考虑:
①CE∥DG;根据抛物线的解析式可求得D点坐标,可得C、D关于抛物线对称轴对称,即C、D的纵坐标相同,所以CD∥x轴,那么C点就是符合条件的G点,易求得CD的长,根据平行四边形的性质知AE=CD,由此可得到AE的长,将A点坐标向左或向右平移CD个单位即可得到两个符合条件的E点坐标;
②AC∥EG;根据平行四边形的性质知,此时G、C的纵坐标互为相反数,由此可求得G点的纵坐标,将其代入抛物线的解析式中即可求得G点的坐标;那么将G点的横坐标减去3(A、C横坐标差的绝对值),即可得到两个符合条件的E点坐标;
综上所述,符合条件的E点坐标应该有4个.
解答:(1)令y=0,则-x2-2x+3=0,
解得:x=-3,x=1,
∴B(-4,0),A(1,0),
∵抛物线y=-x2-2x+3经过C点,C点的横坐标为-2,
∴y=-(-2)2-2×(-2)+3=3,
∴C(-2,3),
设直线AC的解析式为y=kx+b,
∴
,
解得
∴直线AC的解析式为y=-x+1;

(2)设P(m,-m+1),则E(m,-m2-2m+3),
∴PE=-m2-2m+3-(-m+1)=-m2-m+2=-(m+
)2+
,
∴当m=-
时,PE有最大值,最大值为
,
此时P(-
,
),
∴点P坐标为(-
,
)时,线段PE长度有最大值,最大值是
.
(3)存在符合条件的点E,
如图,①在y=-x2-2x+3中,令x=0,则有:y=3,故点D坐标为(0,3),
∴CD∥x轴,
∴在x轴上截取AE1=AE2=CD=2,得四边形ACDE1和ADCE2,
此时:点D与点G重合,E1(-1,0),E2(3,0).
②∵AF=CF=3,∠CFA=90°,
∴∠FAC=45°,
当G3E3∥AC且相等时,有四边形G3E3CA,作G3N⊥x轴于点N,
∵∠G3E3A=∠FAC=45°,∠G3NE3=90°,G3E3=AC=3
,
∴G3N=E3N=3;
将y=-3代入y=-x2-2x+3
得:x=-1+
或x=-1-
,
∴E3的坐标为:(-1+
-3,0),
即(-4+
,0),
同理可得:E4(-4-
,0),
综上所述:存在这样的点E,所有满足条件的E点坐标为:
E1(-1,0),E2(3,0),E3(-4+
,0),E4(-4-
,0).
解得:x=-3,x=1,
∴B(-4,0),A(1,0),
∵抛物线y=-x2-2x+3经过C点,C点的横坐标为-2,
∴y=-(-2)2-2×(-2)+3=3,
∴C(-2,3),
设直线AC的解析式为y=kx+b,
∴
|
解得
|
∴直线AC的解析式为y=-x+1;

(2)设P(m,-m+1),则E(m,-m2-2m+3),
∴PE=-m2-2m+3-(-m+1)=-m2-m+2=-(m+
| 1 |
| 2 |
| 9 |
| 4 |
∴当m=-
| 1 |
| 2 |
| 9 |
| 4 |
此时P(-
| 1 |
| 2 |
| 3 |
| 2 |
∴点P坐标为(-
| 1 |
| 2 |
| 3 |
| 2 |
| 9 |
| 4 |
(3)存在符合条件的点E,
如图,①在y=-x2-2x+3中,令x=0,则有:y=3,故点D坐标为(0,3),
∴CD∥x轴,
∴在x轴上截取AE1=AE2=CD=2,得四边形ACDE1和ADCE2,
此时:点D与点G重合,E1(-1,0),E2(3,0).
②∵AF=CF=3,∠CFA=90°,
∴∠FAC=45°,
当G3E3∥AC且相等时,有四边形G3E3CA,作G3N⊥x轴于点N,
∵∠G3E3A=∠FAC=45°,∠G3NE3=90°,G3E3=AC=3
| 2 |
∴G3N=E3N=3;
将y=-3代入y=-x2-2x+3
得:x=-1+
| 7 |
| 7 |
∴E3的坐标为:(-1+
| 7 |
即(-4+
| 7 |
同理可得:E4(-4-
| 7 |
综上所述:存在这样的点E,所有满足条件的E点坐标为:
E1(-1,0),E2(3,0),E3(-4+
| 7 |
| 7 |
点评:此题考查了二次函数解析式的确定、轴对称的性质以及平行四边形的判定和性质;要特别注意的是(3)题中,由于没有明确AC是平行四边形的边还是对角线,所以一定要分类讨论,以免漏解.

练习册系列答案
 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案
相关题目
若
=a,
=b,则
可以表示为( )
| 3 |
| 5 |
| 45 |
A、
| ||
B、a
| ||
| C、a2b | ||
| D、ab |
 如图所示,抛物线y=x2-2x-3与x轴正半轴交于点A.在对称轴上是否存在点B使得△OAB是等腰三角形?写出所有满足条件的点B的坐标.
如图所示,抛物线y=x2-2x-3与x轴正半轴交于点A.在对称轴上是否存在点B使得△OAB是等腰三角形?写出所有满足条件的点B的坐标. 如图,在坐标网格中,每个小正方形边长为1,△ABC的三个顶点都在格点(小正方形顶点)上.
如图,在坐标网格中,每个小正方形边长为1,△ABC的三个顶点都在格点(小正方形顶点)上. 如图,一工厂的房顶为等腰△ABC,AB=AC,AD=5米,AB=13米,求跨度BC的长.
如图,一工厂的房顶为等腰△ABC,AB=AC,AD=5米,AB=13米,求跨度BC的长. 由于被墨水污染,一道几何题仅能见到如图所示的图形和文字:
由于被墨水污染,一道几何题仅能见到如图所示的图形和文字: