题目内容
14. 在平面直角坐标系中,点A是抛物线y=a(x-3)2+k与y轴的交点,点B是这条抛物线上的另一点,且AB∥x轴,则以AB为边的等边三角形ABC的周长为( )
在平面直角坐标系中,点A是抛物线y=a(x-3)2+k与y轴的交点,点B是这条抛物线上的另一点,且AB∥x轴,则以AB为边的等边三角形ABC的周长为( )| A. | 15 | B. | 18 | C. | 21 | D. | 24 |
分析 根据抛物线解析式求出对称轴为x=3,再根据抛物线的对称性求出AB的长度,然后根据等边三角形三条边都相等列式求解即可.
解答 解:∵抛物线y=a(x-3)2+k的对称轴为x=3,且AB∥x轴,
∴AB=2×3=6,
∴等边△ABC的周长=3×6=18.
故选B.
点评 本题考查了二次函数的性质,等边三角形的周长计算,熟练掌握抛物线的对称轴与两个对称点之间的关系是解题的关键.

练习册系列答案
相关题目
9.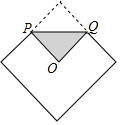 将边长为1的正方形巾的一角折叠至正方形的中心位置,折痕PQ的长为( )
将边长为1的正方形巾的一角折叠至正方形的中心位置,折痕PQ的长为( )
 将边长为1的正方形巾的一角折叠至正方形的中心位置,折痕PQ的长为( )
将边长为1的正方形巾的一角折叠至正方形的中心位置,折痕PQ的长为( )| A. | 1 | B. | 2 | C. | $\frac{\sqrt{2}}{2}$ | D. | $\sqrt{2}$ |
4.YC市首批一次性投放公共自行车700辆供市民租用出行,由于投入数量不够,导致出现需要租用却未租到车的现象,现将随机抽取的某五天在同一时段的调查数据汇成如下表格.
请回答下列问题:
(1)表格中的五个数据(人数)的中位数是多少?
(2)由随机抽样估计,平均每天在7:00-8:00需要租用公共自行车的人数是多少?
请回答下列问题:
| 时间 | 第一天7:00-8:00 | 第二天7:00-8:00 | 第三天7:00-8:00 | 第四天7:00-8:00 | 第五天7:00-8:00 |
| 需要租用自行车却未租到车的人数(人) | 1500 | 1200 | 1300 | 1300 | 1200 |
(2)由随机抽样估计,平均每天在7:00-8:00需要租用公共自行车的人数是多少?
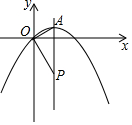 已知:如图,在平面直角坐标系中,抛物线y=ax2+x的对称轴为直线x=2,顶点为A.点P为抛物线对称轴上一点,连结OA、OP.当OA⊥OP时,P点坐标为(2,-4).
已知:如图,在平面直角坐标系中,抛物线y=ax2+x的对称轴为直线x=2,顶点为A.点P为抛物线对称轴上一点,连结OA、OP.当OA⊥OP时,P点坐标为(2,-4).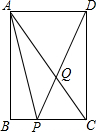 如图,矩形ABCD中,AB=4,AD=3,点Q在对角线AC上,且AQ=AD,连接DQ并延长,与边BC交于点P,则线段AP=$\sqrt{17}$.
如图,矩形ABCD中,AB=4,AD=3,点Q在对角线AC上,且AQ=AD,连接DQ并延长,与边BC交于点P,则线段AP=$\sqrt{17}$.
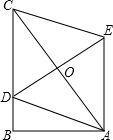 如图,在Rt△ABC中,∠B=90°,AB=5,BC=12,点D在BC上,以AC为对角线的所有平行四边形ADCE中,DE的最小值是( )
如图,在Rt△ABC中,∠B=90°,AB=5,BC=12,点D在BC上,以AC为对角线的所有平行四边形ADCE中,DE的最小值是( )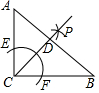 如图,在Rt△ABC中,∠ACB=90°,按以下步骤作图:
如图,在Rt△ABC中,∠ACB=90°,按以下步骤作图: