题目内容
3.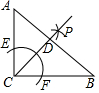 如图,在Rt△ABC中,∠ACB=90°,按以下步骤作图:
如图,在Rt△ABC中,∠ACB=90°,按以下步骤作图:①以C为圆心,以适当长为半径画弧交AC于E,交BC于F.
②分别以E,F为圆心,以大于$\frac{1}{2}$EF的长为半径作弧,两弧相交于P;
③作射线CP交AB于点D,
若AC=3,BC=4,则△ACD的面积为$\frac{18}{7}$.
分析 过点D作DG⊥AC,DH⊥BC,垂足分别为G、H,由题意可知CP是∠ACB的平分线,根据角平分线的性质可知DG=DH,再由三角形的面积公式求出h的值,进而可得出结论.
解答  解:过点D作DG⊥AC,DH⊥BC,垂足分别为G、H,
解:过点D作DG⊥AC,DH⊥BC,垂足分别为G、H,
∵由题意可知CP是∠ACB的平分线,
∴DG=DH.
∵在Rt△ABC中,∠ACB=90°,AC=3,BC=4,
∴S△ABC=S△ACD+S△BCD,即$\frac{1}{2}$×3×4=$\frac{1}{2}$×3DG+$\frac{1}{2}$×4DG,解得DG=$\frac{12}{7}$,
∴△ACD的面积=$\frac{1}{2}$×3×$\frac{12}{7}$=$\frac{18}{7}$.
故答案为:$\frac{18}{7}$.
点评 本题考查的是作图-基本作图,熟知角平分线的作法和性质是解答此题的关键.

练习册系列答案
相关题目
13.下列运算正确的是( )
| A. | a2+a3=a5 | B. | (a3)2÷a6=1 | C. | a2•a3=a6 | D. | ($\sqrt{2}$+$\sqrt{3}$)2=5 |
11.数据2,0,17,6,17的中位数及众数分别是( )
| A. | 0,6 | B. | 2,6 | C. | 6,17 | D. | 2,17 |
8.下表是某校合唱团成员的年龄分布
对于不同的n,下列关于年龄的统计量不会发生改变的是( )
| 年龄/岁 | 13 | 14 | 15 | 16 |
| 频数 | 5 | 15 | 10-n | n |
| A. | 平均数、中位数 | B. | 众数、中位数 | C. | 平均数、方差 | D. | 中位数、方差 |
 在平面直角坐标系中,点A是抛物线y=a(x-3)2+k与y轴的交点,点B是这条抛物线上的另一点,且AB∥x轴,则以AB为边的等边三角形ABC的周长为( )
在平面直角坐标系中,点A是抛物线y=a(x-3)2+k与y轴的交点,点B是这条抛物线上的另一点,且AB∥x轴,则以AB为边的等边三角形ABC的周长为( )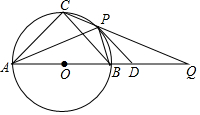 如图,⊙O为等腰△ABC的外接圆,直径AB=12,P为弧$\widehat{BC}$上任意一点(不与B,C重合),直线CP交AB延长线于点Q,⊙O在点P处切线PD交BQ于点D,下列结论正确的是②③④.(写出所有正确结论的序号)
如图,⊙O为等腰△ABC的外接圆,直径AB=12,P为弧$\widehat{BC}$上任意一点(不与B,C重合),直线CP交AB延长线于点Q,⊙O在点P处切线PD交BQ于点D,下列结论正确的是②③④.(写出所有正确结论的序号) 如图,在△ABC中,∠BAD=∠DAC,DF⊥AB,DM⊥AC,AB=16cm,AF=10cm,AC=14cm,动点E以2cm/s的速度从A点向B点运动,动点G以1cm/s的速度从C点向A点运动,当一个点到达终点时,另一个点随之停止运动,设运动时间为t.
如图,在△ABC中,∠BAD=∠DAC,DF⊥AB,DM⊥AC,AB=16cm,AF=10cm,AC=14cm,动点E以2cm/s的速度从A点向B点运动,动点G以1cm/s的速度从C点向A点运动,当一个点到达终点时,另一个点随之停止运动,设运动时间为t.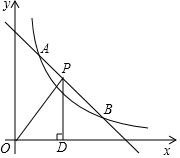 如图,一次函数y=-x+b与反比例函数y=$\frac{k}{x}$(x>0)的图象交于点A(m,3)和B(3,1).
如图,一次函数y=-x+b与反比例函数y=$\frac{k}{x}$(x>0)的图象交于点A(m,3)和B(3,1).