题目内容
 如图,CD是Rt△ABC斜边上的高.
如图,CD是Rt△ABC斜边上的高.(1)求证:∠ACD=∠B;
(2)若AC=3,BC=4,AB=5,则求CD的长.
考点:直角三角形的性质,三角形的面积
专题:
分析:(1)根据垂直的定义和条件可求得∠A+∠ACD=∠A+∠B,可证得结论;
(2)利用面积相等可求得CD.
(2)利用面积相等可求得CD.
解答:(1)证明:∵CD是Rt△ABC斜边上的高,
∴∠ACB=∠ADC=90°,
∴∠A+∠ACD=∠A+∠B=90°,
∴∠ACD=∠B;
(2)解:∵AC=3,BC=4,AB=5,
∴
AB•CD=
AC•BC,
∴CD=
=
=2.4.
∴∠ACB=∠ADC=90°,
∴∠A+∠ACD=∠A+∠B=90°,
∴∠ACD=∠B;
(2)解:∵AC=3,BC=4,AB=5,
∴
| 1 |
| 2 |
| 1 |
| 2 |
∴CD=
| AC•BC |
| AB |
| 3×4 |
| 5 |
点评:本题主要考查直角三角形的性质,掌握直角三角形的两锐角互余是解题的关键.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
 如图,一矩形与⊙O相交,若AB=4,BC=6,DE=2,则DF=( )
如图,一矩形与⊙O相交,若AB=4,BC=6,DE=2,则DF=( )| A、13 | B、12 | C、11 | D、10 |
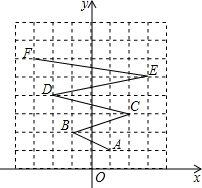 如图,在平面直角坐标系中,一个点从A(a1,a2)出发沿图中路线依次经过B(a3,a4),C(a5,a6),D(a7,a8),…,按此一直运动下去,则a2014+a2015+a2016的值为(
如图,在平面直角坐标系中,一个点从A(a1,a2)出发沿图中路线依次经过B(a3,a4),C(a5,a6),D(a7,a8),…,按此一直运动下去,则a2014+a2015+a2016的值为(| A、1006 | B、1007 |
| C、1509 | D、1511 |
 如图,在△ABC中,CF⊥AB于F,BE⊥AC于E,M为BC的中点.
如图,在△ABC中,CF⊥AB于F,BE⊥AC于E,M为BC的中点. 如图是某地气温t(℃)随着高度h(千米)的增加而降低的关系图,观察图象可知该地地面气温是
如图是某地气温t(℃)随着高度h(千米)的增加而降低的关系图,观察图象可知该地地面气温是 甲、乙两人用如图所示的两个分格均匀的转盘做游戏:分别转动两个转盘,若转盘停止后,指针指向一个数字(若指针恰好停在分格线上,则重转一次),用所指的两个数字作乘积,如果积大于10,那么甲获胜;如果积不大于10,那么乙获胜.清你解决下列问题:
甲、乙两人用如图所示的两个分格均匀的转盘做游戏:分别转动两个转盘,若转盘停止后,指针指向一个数字(若指针恰好停在分格线上,则重转一次),用所指的两个数字作乘积,如果积大于10,那么甲获胜;如果积不大于10,那么乙获胜.清你解决下列问题: 如图已知△ABC,
如图已知△ABC, 如图,已知CF⊥AB于点E,且AE=EB,∠B=40°.求∠ACD、∠DCF的度数.
如图,已知CF⊥AB于点E,且AE=EB,∠B=40°.求∠ACD、∠DCF的度数. 如图,已知两直线相交,∠1=30°,则∠3=
如图,已知两直线相交,∠1=30°,则∠3=