题目内容
1.计算:3$\sqrt{3}$-$\sqrt{12}$=$\sqrt{3}$;(2+$\sqrt{3}$)(2-$\sqrt{3}$)=1.$\sqrt{2}$($\sqrt{2}+\sqrt{3}$)=2+$\sqrt{6}$;($\sqrt{80}$+$\sqrt{40}$)÷$\sqrt{5}$=4+2$\sqrt{2}$.
分析 先进行二次根式的化简,然后合并;
根据平方差公式求解;
直接进行二次根式的乘法运算;
先进行二次根式的除法运算,然后合并.
解答 解:原式=3$\sqrt{3}$-2$\sqrt{3}$
=$\sqrt{3}$;
原式=4-3
=1;
原式=2+$\sqrt{6}$;
原式=$\sqrt{16}$+$\sqrt{8}$
=4+2$\sqrt{2}$.
故答案为:$\sqrt{3}$;1;2+$\sqrt{6}$;4+2$\sqrt{2}$.
点评 本题考查了二次根式的混合运算,解答本题的关键是掌握二次根式的乘法法则和除法法则和平方差公式.

练习册系列答案
相关题目
16.下列计算中,正确的是( )
| A. | 2$\sqrt{3}$-$\sqrt{3}$=2 | B. | 2+$\sqrt{2}$=2$\sqrt{2}$ | C. | $\sqrt{8}$-$\sqrt{2}$=$\sqrt{2}$ | D. | $\sqrt{9}$-$\sqrt{4}$=$\sqrt{5}$ |
10.下列图形是中心对称图形但不是轴对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
 如图,△ABC与△ADE都是等腰直角三角形,且∠BAC=∠DAE=90°,请找出一条与线段CE相等的线段(以图中已知点的端点),画出这条线段并给出证明.
如图,△ABC与△ADE都是等腰直角三角形,且∠BAC=∠DAE=90°,请找出一条与线段CE相等的线段(以图中已知点的端点),画出这条线段并给出证明.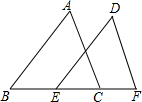 如图,已知:∠B=∠DEF,BC=EF,现要证明△ABC≌△DEF,若要以“SAS”为依据,还缺条件AB=DE;若要以“ASA”为依据,还缺条件∠ACB=∠DFE,若要以“AAS”为依据,还缺条件∠A=∠D.
如图,已知:∠B=∠DEF,BC=EF,现要证明△ABC≌△DEF,若要以“SAS”为依据,还缺条件AB=DE;若要以“ASA”为依据,还缺条件∠ACB=∠DFE,若要以“AAS”为依据,还缺条件∠A=∠D.