题目内容
12. 如图,△ABC与△ADE都是等腰直角三角形,且∠BAC=∠DAE=90°,请找出一条与线段CE相等的线段(以图中已知点的端点),画出这条线段并给出证明.
如图,△ABC与△ADE都是等腰直角三角形,且∠BAC=∠DAE=90°,请找出一条与线段CE相等的线段(以图中已知点的端点),画出这条线段并给出证明.
分析 连接BD,则BD=CE,证明△AEC≌△ADB即可.
解答 解:连接BD,则BD=CE;
理由:∵△ABC与△ADE都是等腰直角三角形,
∴AB=AC,AE=AD,
∵∠BAC=∠DAE=90°,
∴∠BAD=∠CAE,
在△AEC和△ADB中,
$\left\{\begin{array}{l}{AB=AC}\\{∠BAD=∠CAE}\\{AD=AE}\end{array}\right.$,
∴△AEC≌△ADB(SAS),
∴BD=CE.
点评 本题考查了全等三角形的判定与性质,熟练掌握全等三角形的判定与性质是解决问题的关键.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
2.下列调查,最适合使用普查方式的是( )
| A. | 为制作校服,了解某班同学的身高情况 | |
| B. | 了解全市每天丢弃的废旧电池数 | |
| C. | 了解某批炮弹的杀伤半径 | |
| D. | 了解我省农民的年人均收入情况 |
 +(
+( +
+ )(
)(  -2
-2 )-(
)-( -
- ,其中
,其中 =-3,
=-3,  =
= .
.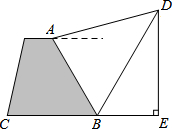 如图,小明站在看台上的A处,测得旗杆顶端D的仰角为15°,当旗杆顶端D的影子刚好落在看台底部B处时,太阳光与地面成60°角.已知∠ABC=60°,AB=4米,求旗杆的高度.(点A与旗杆DE及其影子在同一平面内,C、B、E三点共线且旗杆与地面垂直,不考虑小明的身高)
如图,小明站在看台上的A处,测得旗杆顶端D的仰角为15°,当旗杆顶端D的影子刚好落在看台底部B处时,太阳光与地面成60°角.已知∠ABC=60°,AB=4米,求旗杆的高度.(点A与旗杆DE及其影子在同一平面内,C、B、E三点共线且旗杆与地面垂直,不考虑小明的身高) 如图所示,已知?ABCD中,E、F分别是对角线AC延长线上的点,且DE=BF,四边形BFDE是平行四边形吗?说说你的理由.
如图所示,已知?ABCD中,E、F分别是对角线AC延长线上的点,且DE=BF,四边形BFDE是平行四边形吗?说说你的理由.