题目内容
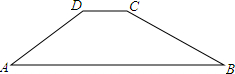 如图,某一大坝的横断面是梯形ABCD,坝顶宽CD=6米,斜坡AD=16米,坝高8米,斜坡BC的坡度i=1:3,则坝底宽AB是( )米.
如图,某一大坝的横断面是梯形ABCD,坝顶宽CD=6米,斜坡AD=16米,坝高8米,斜坡BC的坡度i=1:3,则坝底宽AB是( )米.A、24+8
| ||
| B、30 | ||
C、30+8
| ||
D、30+16
|
考点:解直角三角形的应用-坡度坡角问题
专题:
分析:过D点作DE⊥AB于点E,过C点作CF⊥AB于点F,得到两个直角三角形和一个矩形,在Rt△AED中利用DE和AD的长,求得线段AE的长;在Rt△BCF中利用BC的坡度和CF的长求得线段BF的长,然后与AE、EF相加即可求得AB的长.
解答: 解:过D点作DE⊥AB于点E,过C点作CF⊥AB于点F,则四边形CDEF是矩形
解:过D点作DE⊥AB于点E,过C点作CF⊥AB于点F,则四边形CDEF是矩形
∴CD=FE=6m,CF=ED=8m,
在Rt△AED中,AE=
=8
m,
∵CF:BF=1:3,
∴BF=3CF=24m,
即AB=BF+EF+AE=24+6+8
=(30+8
)米.
故选C.
 解:过D点作DE⊥AB于点E,过C点作CF⊥AB于点F,则四边形CDEF是矩形
解:过D点作DE⊥AB于点E,过C点作CF⊥AB于点F,则四边形CDEF是矩形∴CD=FE=6m,CF=ED=8m,
在Rt△AED中,AE=
| 162-82 |
| 3 |
∵CF:BF=1:3,
∴BF=3CF=24m,
即AB=BF+EF+AE=24+6+8
| 3 |
| 3 |
故选C.
点评:此题主要考查了解直角三角形的应用,解决本题的关键是利用锐角三角函数的概念和坡度的概念求解.

练习册系列答案
相关题目
按一定规律排列的一组数:
,
,
,
,…,
,
,
,…(其中x,y为整数),则x+y=( )
| 1 |
| 2 |
| 1 |
| 6 |
| 1 |
| 12 |
| 1 |
| 20 |
| 1 |
| x |
| 1 |
| 90 |
| 1 |
| y |
| A、172 | B、182 |
| C、200 | D、242 |
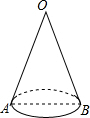 如图是一个圣诞帽,已知开口圆的直径AB长为10cm,母线OA长为20cm.从开口的A点出发,用一根彩带绕侧面一周回到A点,则彩带最短需要( )
如图是一个圣诞帽,已知开口圆的直径AB长为10cm,母线OA长为20cm.从开口的A点出发,用一根彩带绕侧面一周回到A点,则彩带最短需要( )| A、20cm | ||
B、20
| ||
| C、30cm | ||
D、20
|
 如图,△ABC的BC边与⊙O相切于B点,若直径AB=BC=4,则AC的值是( )
如图,△ABC的BC边与⊙O相切于B点,若直径AB=BC=4,则AC的值是( )A、2
| ||
B、2
| ||
C、4
| ||
D、4
|
如果5x3m-2n-2yn-m=2是关于x,y的二元一次方程,那么( )
| A、m=1,n=2 |
| B、m=2,n=-3 |
| C、m=3,n=4 |
| D、m=2,n=2 |
下列计算正确的是( )
| A、a3-a=a2 |
| B、(-2013)0=1 |
| C、a6÷a2=a3 |
| D、(a+2)2=a2+4 |


 如图,正方形网格中的每个小正方形边长都为1,每个小正方形的顶点叫格点,按要求画一个三角形:使这个三角形的顶点都在格点上,该三角形的面积为3,且有一边长为
如图,正方形网格中的每个小正方形边长都为1,每个小正方形的顶点叫格点,按要求画一个三角形:使这个三角形的顶点都在格点上,该三角形的面积为3,且有一边长为 如图,平面直角坐标系中,△ABC的顶点都在正方形(每个小正方形边长为单位1)网格的格点上.
如图,平面直角坐标系中,△ABC的顶点都在正方形(每个小正方形边长为单位1)网格的格点上.