题目内容
在学习了投影知识后,小刚和小亮利用“同一时刻太阳光下物长与影长成比例”的原理测得某棵大树的高为8米,当他们又一次经过这棵大树时,发现大树的影子落在了有个圆弧形小桥的路上,小刚突发奇想:能不能测出这个圆弧形小桥所在圆的半径呢?请你也加入他们的行列,测出小桥的半径吧!

(1)如图,AB为小亮、BC为他的影子,DE为大树,请你在图中画出这棵大树的影子(影子的另一个端点用F表示),尺规作图,保留作图痕迹;
(2)在(1)的基础上,已知小亮的身高AB为1.6米,测得小亮的影长BC为2.4米,同一时刻测得EG的长为2.5米,HF的长为1.5米,又测得小桥的拱高(弦GH的中点与
的中点之间的距离)为2米,求圆弧形小桥所在圆的半径.

(1)如图,AB为小亮、BC为他的影子,DE为大树,请你在图中画出这棵大树的影子(影子的另一个端点用F表示),尺规作图,保留作图痕迹;
(2)在(1)的基础上,已知小亮的身高AB为1.6米,测得小亮的影长BC为2.4米,同一时刻测得EG的长为2.5米,HF的长为1.5米,又测得小桥的拱高(弦GH的中点与
 |
| GH |
考点:相似三角形的应用,勾股定理,垂径定理的应用
专题:
分析:(1)连接AC,以点D为顶点,DE为一边作∠D=∠A,∠D的另一边与直线EH相交于F,EF即为大树的影子;
(2)先根据同时同地的物高与影长成正比求出大树的影长,再求出GH,然后根据垂径定理,利用勾股定理列式计算即可得解.
(2)先根据同时同地的物高与影长成正比求出大树的影长,再求出GH,然后根据垂径定理,利用勾股定理列式计算即可得解.
解答: 解:(1)如图所示,EF即为大树的影子;
解:(1)如图所示,EF即为大树的影子;
(2)根据题意得,
=
,
即
=
,
解得EF=12,
∵EG的长为2.5米,HF的长为1.5米,
∴GH=12-2.5-1.5=8,
设圆弧形小桥所在圆的半径为r,
则(
)2+(r-2)2=r2,
解得r=5,
答:圆弧形小桥所在圆的半径为5米.
 解:(1)如图所示,EF即为大树的影子;
解:(1)如图所示,EF即为大树的影子;(2)根据题意得,
| EF |
| DE |
| BC |
| AB |
即
| EF |
| 8 |
| 2.4 |
| 1.6 |
解得EF=12,
∵EG的长为2.5米,HF的长为1.5米,
∴GH=12-2.5-1.5=8,
设圆弧形小桥所在圆的半径为r,
则(
| 8 |
| 2 |
解得r=5,
答:圆弧形小桥所在圆的半径为5米.
点评:本题考查了相似三角形的应用,垂径定理的应用,考虑到作平行线是解题的关键.

练习册系列答案
相关题目
2013年元月以来,雾霾天气严重影响道路交通,影响人们的正常生活.小明连续两天了解了附近两个城市的天气情况:A城市和B城市两天中均有一天是雾霾天气.则从中任意抽取一天,两个城市都不是雾霾天气的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
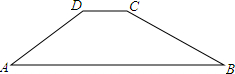 如图,某一大坝的横断面是梯形ABCD,坝顶宽CD=6米,斜坡AD=16米,坝高8米,斜坡BC的坡度i=1:3,则坝底宽AB是( )米.
如图,某一大坝的横断面是梯形ABCD,坝顶宽CD=6米,斜坡AD=16米,坝高8米,斜坡BC的坡度i=1:3,则坝底宽AB是( )米.A、24+8
| ||
| B、30 | ||
C、30+8
| ||
D、30+16
|
 为了进一步丰富校园文化生活,某校举办了校园文化艺术节.小颖为了了解同学们对这次艺术节的评价,对该校的部分学生进行调查(共有很好、好、一般、不好四种评价),并绘制了如下尚不完整的统计表与扇形统计图.
为了进一步丰富校园文化生活,某校举办了校园文化艺术节.小颖为了了解同学们对这次艺术节的评价,对该校的部分学生进行调查(共有很好、好、一般、不好四种评价),并绘制了如下尚不完整的统计表与扇形统计图.
 观察如图所示图形的构成规律,根据此规律,共有96个圆的是第
观察如图所示图形的构成规律,根据此规律,共有96个圆的是第