题目内容
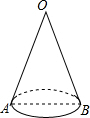 如图是一个圣诞帽,已知开口圆的直径AB长为10cm,母线OA长为20cm.从开口的A点出发,用一根彩带绕侧面一周回到A点,则彩带最短需要( )
如图是一个圣诞帽,已知开口圆的直径AB长为10cm,母线OA长为20cm.从开口的A点出发,用一根彩带绕侧面一周回到A点,则彩带最短需要( )| A、20cm | ||
B、20
| ||
| C、30cm | ||
D、20
|
考点:平面展开-最短路径问题,圆锥的计算
专题:
分析:先求出圆锥底面周长,将图形展开,过点O作OD⊥AB于点D,设圆心角∠BOA=n°,由弧长公式可求出n的值,故可得出∠OAB的度数,根据锐角三角函数的定义求出AD的长,故可得出AB的长.
解答: 解:∵开口圆的直径AB长为10cm,
解:∵开口圆的直径AB长为10cm,
∴圆锥底面周长为2π×5=10πcm,
展开后为扇形,如图所示:
过点O作OD⊥AB于点D,
∵母线长为20cm,设圆心角∠BOA=n°,
∴10π=
,
解得n=90°,
∴∠OAB=∠OBA=(180°-90°)÷2=45°,
∴AD=AO•cos45°=20×
=10
cm,
∴AB=10
×2=20
cm.
故选B.
 解:∵开口圆的直径AB长为10cm,
解:∵开口圆的直径AB长为10cm,∴圆锥底面周长为2π×5=10πcm,
展开后为扇形,如图所示:
过点O作OD⊥AB于点D,
∵母线长为20cm,设圆心角∠BOA=n°,
∴10π=
| 20nπ |
| 180 |
解得n=90°,
∴∠OAB=∠OBA=(180°-90°)÷2=45°,
∴AD=AO•cos45°=20×
| ||
| 2 |
| 2 |
∴AB=10
| 2 |
| 2 |
故选B.
点评:本题考查的是平面展开-最短路径问题,根据题意画出圆锥的侧面展开图是解答此题的关键.

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案
相关题目
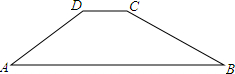 如图,某一大坝的横断面是梯形ABCD,坝顶宽CD=6米,斜坡AD=16米,坝高8米,斜坡BC的坡度i=1:3,则坝底宽AB是( )米.
如图,某一大坝的横断面是梯形ABCD,坝顶宽CD=6米,斜坡AD=16米,坝高8米,斜坡BC的坡度i=1:3,则坝底宽AB是( )米.A、24+8
| ||
| B、30 | ||
C、30+8
| ||
D、30+16
|
若(1-2a)2+
=0,则ab的值为( )
| b+2 |
| A、-2 | ||
B、
| ||
| C、-1 | ||
| D、1 |
下列数字中是中心对称的是( )
A、 |
B、 |
C、 |
D、 |
 为了进一步丰富校园文化生活,某校举办了校园文化艺术节.小颖为了了解同学们对这次艺术节的评价,对该校的部分学生进行调查(共有很好、好、一般、不好四种评价),并绘制了如下尚不完整的统计表与扇形统计图.
为了进一步丰富校园文化生活,某校举办了校园文化艺术节.小颖为了了解同学们对这次艺术节的评价,对该校的部分学生进行调查(共有很好、好、一般、不好四种评价),并绘制了如下尚不完整的统计表与扇形统计图. 观察如图所示图形的构成规律,根据此规律,共有96个圆的是第
观察如图所示图形的构成规律,根据此规律,共有96个圆的是第