题目内容
如图，平面直角坐标系中，△ABC的顶点都在正方形（每个小正方形边长为单位1）网格的格点上．（1）画出△ABC沿x轴翻折后的△A1B1C1．
（2）画出△ABC绕点B顺时针旋转90°后的△BA2C2，并求出旋转过程中点A经过的路径长．（结果保留π）
考点：作图-旋转变换,作图-轴对称变换
专题：作图题
分析：（1）根据网格结构找出点A、B、C关于x轴的对称点A1、B1、C1的位置，然后顺次连接即可；
（2）根据勾股定理列式求出AB的长度，然后根据弧长公式列式计算即可得解．
（2）根据勾股定理列式求出AB的长度，然后根据弧长公式列式计算即可得解．
解答：
解：（1）△A1B1C1如图所示；
（2）根据勾股定理，AB=
=
，
所以，点A经过的路径长=
=
π．
解：（1）△A1B1C1如图所示；（2）根据勾股定理，AB=
| 12+32 |
| 10 |
所以，点A经过的路径长=
90•π•
| ||
| 180 |
| ||
| 2 |
点评：本题考查了利用轴对称变换作图，利用旋转变换作图，以及弧长的计算，熟练掌握网格结构，准确找出对应顶点的位置是解题的关键．
练习册系列答案
云南师大附小一线名师提优作业系列答案
冲刺100分单元优化练考卷系列答案
相关题目
观察如图所示图形的构成规律，根据此规律，共有96个圆的是第
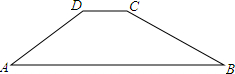如图，某一大坝的横断面是梯形ABCD，坝顶宽CD=6米，斜坡AD=16米，坝高8米，斜坡BC的坡度i=1：3，则坝底宽AB是（ ）米．A、24+8
| ||
| B、30 | ||
C、30+8
| ||
D、30+16
|
若（1-2a）2+
=0，则ab的值为（ ）
| b+2 |
| A、-2 | ||
B、
| ||
| C、-1 | ||
| D、1 |
下列数字中是中心对称的是（ ）
A、 |
B、 |
C、 |
D、 |