题目内容
按一定规律排列的一组数:
,
,
,
,…,
,
,
,…(其中x,y为整数),则x+y=( )
| 1 |
| 2 |
| 1 |
| 6 |
| 1 |
| 12 |
| 1 |
| 20 |
| 1 |
| x |
| 1 |
| 90 |
| 1 |
| y |
| A、172 | B、182 |
| C、200 | D、242 |
考点:规律型:数字的变化类
专题:规律型
分析:观察各数据得到
=
,
=
,
=
,
=
,即每个分数的分母可以分解为两个连续正整数的积,由于
=
,所以
=
,
=
,即可得到x与y的值.
| 1 |
| 2 |
| 1 |
| 1×2 |
| 1 |
| 6 |
| 1 |
| 2×3 |
| 1 |
| 12 |
| 1 |
| 3×4 |
| 1 |
| 20 |
| 1 |
| 4×5 |
| 1 |
| 90 |
| 1 |
| 9×10 |
| 1 |
| x |
| 1 |
| 8×9 |
| 1 |
| y |
| 1 |
| 10×11 |
解答:解:∵
=
,
=
,
=
,
=
,
而
=
,
∴
=
,
=
,
∴x=72,y=110,
∴x+y=72+110=182.
故选C.
| 1 |
| 2 |
| 1 |
| 1×2 |
| 1 |
| 6 |
| 1 |
| 2×3 |
| 1 |
| 12 |
| 1 |
| 3×4 |
| 1 |
| 20 |
| 1 |
| 4×5 |
而
| 1 |
| 90 |
| 1 |
| 9×10 |
∴
| 1 |
| x |
| 1 |
| 8×9 |
| 1 |
| y |
| 1 |
| 10×11 |
∴x=72,y=110,
∴x+y=72+110=182.
故选C.
点评:本题考查了规律型:数字的变化类:通过从一些特殊的数字变化中发现不变的因素或按规律变化的因素,然后推广到一般情况.

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案
相关题目
若
+
=2,则
的值等于( )
| b |
| a |
| a |
| b |
| a2+ab+b2 |
| a2+4ab+b2 |
| A、2 | ||
| B、-2 | ||
C、
| ||
D、-
|
下列运算中,正确的是( )
| A、a3•a2=a6 | ||||||
| B、(x3)3=x6 | ||||||
| C、(-a)3=-a3 | ||||||
D、
|
2013年元月以来,雾霾天气严重影响道路交通,影响人们的正常生活.小明连续两天了解了附近两个城市的天气情况:A城市和B城市两天中均有一天是雾霾天气.则从中任意抽取一天,两个城市都不是雾霾天气的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
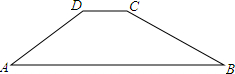 如图,某一大坝的横断面是梯形ABCD,坝顶宽CD=6米,斜坡AD=16米,坝高8米,斜坡BC的坡度i=1:3,则坝底宽AB是( )米.
如图,某一大坝的横断面是梯形ABCD,坝顶宽CD=6米,斜坡AD=16米,坝高8米,斜坡BC的坡度i=1:3,则坝底宽AB是( )米.A、24+8
| ||
| B、30 | ||
C、30+8
| ||
D、30+16
|