题目内容
13.小丽乘坐汽车去奶奶家,她去时经过高速公路,全程84km,返回时经过跨海大桥,全程45km,小丽所乘汽车去时平均速度是返回时的1.2倍,所用时间却返回时多20分钟,求小丽所乘汽车返回时的平均速度为多少千米/时?分析 设小丽所乘汽车返回时的平均速度是x千米/时,则去时的速度是1.2x千米/时,根据题意可得等量关系:去时所用的时间-回来时所用的时间=20分钟,根据等量关系可得方程$\frac{84}{1.2x}$-$\frac{45}{x}$=$\frac{20}{60}$,再解方程即可.
解答 解:设小丽所乘汽车返回时的平均速度是x千米/时,根据题意得:
$\frac{84}{1.2x}$-$\frac{45}{x}$=$\frac{20}{60}$,
解这个方程,得:x=75,
经检验,x=75是原方程的解.
答:小丽所乘汽车返回时的速度是75千米/时.
点评 此题主要考查了分式方程的应用,关键是正确理解题意,找出题目中的等量关系,列出方程,注意不要忘记检验.

练习册系列答案
 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目
3.在一个不透明的口袋中装有5个完全相同的小球,把它们分别标号为1,2,3,4,5,从中随机摸出一个小球,其标号是奇数的概率为( )
| A. | $\frac{1}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
4.下列各数中与$\sqrt{2}$是同类二次根式的是( )
| A. | $\sqrt{2}$ | B. | $\root{3}{2}$ | C. | $\sqrt{4}$ | D. | $\sqrt{12}$ |
1.下面计算正确的是( )
| A. | a+a-1=0 | B. | ($\sqrt{2}$+1)(1-$\sqrt{2}$)=1 | C. | (xy)-1($\frac{1}{2}$xy)2=$\frac{1}{4}$xy | D. | -(-a)4÷a2=a2 |
5.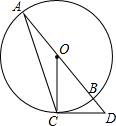 如图,AB是⊙O的直径,点C在⊙O上,过点C作⊙O的切线交AB的延长线于点D,连接OC,AC.若∠D=50°,则∠A的度数是( )
如图,AB是⊙O的直径,点C在⊙O上,过点C作⊙O的切线交AB的延长线于点D,连接OC,AC.若∠D=50°,则∠A的度数是( )
 如图,AB是⊙O的直径,点C在⊙O上,过点C作⊙O的切线交AB的延长线于点D,连接OC,AC.若∠D=50°,则∠A的度数是( )
如图,AB是⊙O的直径,点C在⊙O上,过点C作⊙O的切线交AB的延长线于点D,连接OC,AC.若∠D=50°,则∠A的度数是( )| A. | 20° | B. | 25° | C. | 40° | D. | 50° |
2.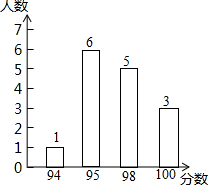 某次比赛中,15名选手的成绩如图所示,则这15名选手成绩的众数和中位数分别是( )
某次比赛中,15名选手的成绩如图所示,则这15名选手成绩的众数和中位数分别是( )
 某次比赛中,15名选手的成绩如图所示,则这15名选手成绩的众数和中位数分别是( )
某次比赛中,15名选手的成绩如图所示,则这15名选手成绩的众数和中位数分别是( )| A. | 98,95 | B. | 98,98 | C. | 95,98 | D. | 95,95 |
3.下列图形中,既是轴对称图形又是中心对称图形的是( )
| A. | 平行四边形 | B. | 圆 | C. | 正五边形 | D. | 等腰三角形 |
 如图,△AED∽△ACB,△AED的面积为△ACB面积的$\frac{1}{3}$,则AD:AB=$\sqrt{3}$:3.
如图,△AED∽△ACB,△AED的面积为△ACB面积的$\frac{1}{3}$,则AD:AB=$\sqrt{3}$:3. 如图,在坐标系中放置一菱形OABC,已知∠ABC=60°,OA=1.先将菱形OABC沿x轴的正方向无滑动翻转,每次翻转60°,连续翻转2015次,点B的落点依次为B1,B2,B3,…,则B2015的坐标为(1342.5,$\frac{\sqrt{3}}{2}$).
如图,在坐标系中放置一菱形OABC,已知∠ABC=60°,OA=1.先将菱形OABC沿x轴的正方向无滑动翻转,每次翻转60°,连续翻转2015次,点B的落点依次为B1,B2,B3,…,则B2015的坐标为(1342.5,$\frac{\sqrt{3}}{2}$).