题目内容
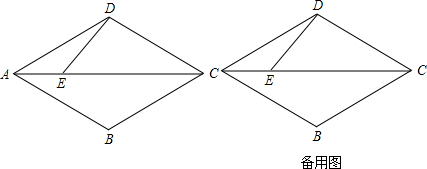
18. 如图,在坐标系中放置一菱形OABC,已知∠ABC=60°,OA=1.先将菱形OABC沿x轴的正方向无滑动翻转,每次翻转60°,连续翻转2015次,点B的落点依次为B1,B2,B3,…,则B2015的坐标为(1342.5,$\frac{\sqrt{3}}{2}$).
如图,在坐标系中放置一菱形OABC,已知∠ABC=60°,OA=1.先将菱形OABC沿x轴的正方向无滑动翻转,每次翻转60°,连续翻转2015次,点B的落点依次为B1,B2,B3,…,则B2015的坐标为(1342.5,$\frac{\sqrt{3}}{2}$).
分析 连接AC,根据条件可以求出AC,画出第5次、第6次、第7次翻转后的图形,容易发现规律:每翻转6次,图形向右平移4.由于2015=335×6+5,因此点B5向右平移1340(即335×4)即可到达点B2015,根据点B5的坐标就可求出点B2015的坐标.
解答 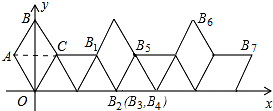 解:连接AC,如图所示.
解:连接AC,如图所示.
∵四边形OABC是菱形,
∴OA=AB=BC=OC.
∵∠ABC=60°,
∴△ABC是等边三角形.
∴AC=AB.
∴AC=OA.
∵OA=1,
∴AC=1.
画出第5次、第6次、第7次翻转后的图形,如图所示.
由图可知:每翻转6次,图形向右平移4.
∵2015=335×6+5,
∴点B5向右平移1340(即335×4)到点B2014.
∵B5的坐标为(2.5,$\frac{\sqrt{3}}{2}$),
∴B2014的坐标为(2.5+1340,$\frac{\sqrt{3}}{2}$),
∴B2015的坐标为(1342.5,$\frac{\sqrt{3}}{2}$).
故答案为:(1342.5,$\frac{\sqrt{3}}{2}$).
点评 本题考查了菱形的性质、等边三角形的判定与性质等知识,考查了操作、探究、发现规律的能力.发现“每翻转6次,图形向右平移4”是解决本题的关键.

练习册系列答案
 活力课时同步练习册系列答案
活力课时同步练习册系列答案 学业测评一课一测系列答案
学业测评一课一测系列答案
相关题目
8.某校学生参加体育测试,某小组10名同学的完成引体向上的个数如下表,
这10名同学引体向上个数的众数与中位数依次是( )
| 完成引体向上的个数 | 10 | 9 | 8 | 7 |
| 人 数 | 1 | 1 | 3 | 5 |
| A. | 7和7.5 | B. | 7和8 | C. | 7.5和9 | D. | 8和9 |
3.在六张卡片上分别写有π,$\frac{1}{3}$,1.5,-3,0,$\sqrt{2}$六个数,从中任意抽取一张,卡片上的数为无理数的概率是( )
| A. | $\frac{1}{6}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
10.北京的水资源非常匮乏,为促进市民节水,从2014年5月1日起北京市居民用水实行阶梯水价,实施细则如表:
北京市居民用水阶梯水价表 单位:元/立方米
某户居民从2015年1月1日至4月30日,累积用水190立方米,则这户居民4个月共需缴纳水费970元.
北京市居民用水阶梯水价表 单位:元/立方米
| 分档水量 | 户年用水量 (立方米) | 水价 | 其中 | ||
| 自来水费 | 水资源费 | 污水 处理费 | |||
| 第一阶梯 | 0-180(含) | 5.00 | 2.07 | 1.57 | 1.36 |
| 第二阶梯 | 181-260(含) | 7.00 | 4.07 | ||
| 第三阶梯 | 260以上 | 9.00 | 6.07 | ||
8.一个圆锥的侧面积是底面积的2倍,则圆锥侧面积展开的扇形圆心角的度数是( )
| A. | 300° | B. | 240° | C. | 180° | D. | 120° |
 如图,某小区规划在一个长80m、宽50m的长方形ABCD上修建三条同样宽的通道,使其中两条与AB平行,另一条与AD平行,其余部分种花草,使花草的种植面积共为3800m2.设通道的宽为xm,可依题意列得方程:(80-2x)(50-x)=3800.
如图,某小区规划在一个长80m、宽50m的长方形ABCD上修建三条同样宽的通道,使其中两条与AB平行,另一条与AD平行,其余部分种花草,使花草的种植面积共为3800m2.设通道的宽为xm,可依题意列得方程:(80-2x)(50-x)=3800.