题目内容
15. 按要求解答下列各小题
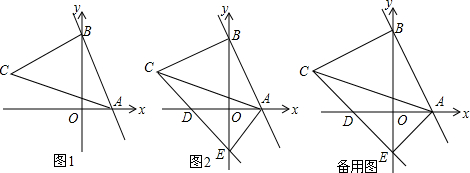
按要求解答下列各小题(1)如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(-2,1),B(-1,4),C(-3,2).以原点O为位似中心,位似比为1:2,在y轴的左侧,画出△ABC放大后的图形△A1B1C1,并直接写出C1点坐标;
(2)某班排球兴趣小组4名学生中有3男1女,现在打算从中随机选出2名学生参加学校的排球队,请用列表或画树状图的方法求选出的2名学生恰好是1男1女的概率.
分析 (1)根据以原点O为位似中心的坐标变换规律,把A、B、C的横纵坐标都乘以2即可得到A1、B1、C1的坐标,然后描点即可得到△A1B1C1;
(2)利用树状图展示所有12种等可能的结果数,再找出选出的2名学生恰好是1男1女的结果数,然后根据概率公式求解.
解答 解:(1)如图,△A1B1C1为所作,C1点坐标为(-6,4);
(2)画树状图为:
共有12种等可能的结果数,其中选出的2名学生恰好是1男1女的结果数为6,
所以选出的2名学生恰好是1男1女的概率=$\frac{6}{12}$=$\frac{1}{2}$.
点评 本题考查了作图-位似变换:画位似图形的一般步骤为:先确定位似中心;再分别连接并延长位似中心和能代表原图的关键点;接着根据位似比,确定能代表所作的位似图形的关键点;然后顺次连接上述各点,得到放大或缩小的图形.也考查了列表法与树状图法.

练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目
3.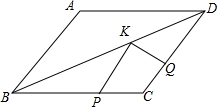 如图,△ABD≌△CDB,且∠ADB=∠ABD,△ABD的面积是2$\sqrt{3}$,AB=2,点P,Q,K分别为线段BC,CD,BD上的任意一点,则PK+QK的最小值为( )
如图,△ABD≌△CDB,且∠ADB=∠ABD,△ABD的面积是2$\sqrt{3}$,AB=2,点P,Q,K分别为线段BC,CD,BD上的任意一点,则PK+QK的最小值为( )
 如图,△ABD≌△CDB,且∠ADB=∠ABD,△ABD的面积是2$\sqrt{3}$,AB=2,点P,Q,K分别为线段BC,CD,BD上的任意一点,则PK+QK的最小值为( )
如图,△ABD≌△CDB,且∠ADB=∠ABD,△ABD的面积是2$\sqrt{3}$,AB=2,点P,Q,K分别为线段BC,CD,BD上的任意一点,则PK+QK的最小值为( )| A. | $\sqrt{3}$ | B. | 4 | C. | 2 | D. | 2$\sqrt{3}$ |