题目内容
3.以(2,3)为顶点且开口向下的二次函数的解析式为y=-(x-2)2+3(写出一个即可).分析 根据题意抛物线的顶点坐标是(2,3),故设出抛物线的顶点式方程y=a(x-2)2+3,再有开口向下可知a<0,故可取a=-1,即得结果.
解答 解:∵抛物线的顶点坐标为(2,3)
∴可设抛物线的解析式为y=a(x-2)2+3,
又∵抛物线的开口向下,
∴a<0,故可取a=-1,
∴抛物线的解析式为y=-(x-2)2+3.
故答案为:y=-(x-2)2+3.
点评 此题考查了二次函数的解析式的求法,关键是要由顶点坐标正确设出抛物线的解析式.理解开口向下的含义.

练习册系列答案
相关题目
14.已知平行四边形的一边长为10,则对角线的长度可能取下列数组中的( )
| A. | 4、8 | B. | 8、6 | C. | 8、10 | D. | 11、13 |
11.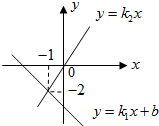 直线l1:y=k1x+b与直线l2:y=k2x在同一平面直角坐标系中的图象如图所示,则关于x的不等式k1x+b>k2x的解为( )
直线l1:y=k1x+b与直线l2:y=k2x在同一平面直角坐标系中的图象如图所示,则关于x的不等式k1x+b>k2x的解为( )
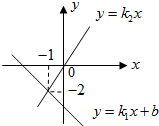 直线l1:y=k1x+b与直线l2:y=k2x在同一平面直角坐标系中的图象如图所示,则关于x的不等式k1x+b>k2x的解为( )
直线l1:y=k1x+b与直线l2:y=k2x在同一平面直角坐标系中的图象如图所示,则关于x的不等式k1x+b>k2x的解为( )| A. | x>-1 | B. | x<-1 | C. | x<-2 | D. | 无法确定 |
15.点A关于原点对称的点的坐标是(3,-6),则点A的坐标是( )
| A. | (3,6) | B. | (-3,6) | C. | (3,-6) | D. | (-3,-6) |
13. 作一个已知角的平分线的作图依据是( )
作一个已知角的平分线的作图依据是( )
 作一个已知角的平分线的作图依据是( )
作一个已知角的平分线的作图依据是( )| A. | SAS | B. | AAS | C. | ASA | D. | SSS |
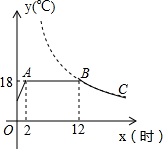 某蔬菜生产基地在气温较低时,用装有恒温系统的大棚栽培一种在自然光照且温度为18℃的条件下生长最快的新品种,下图是某天恒温系统从开启到关闭及关闭后,大棚内温度y(℃)随时间x(小时)变化的函数图象,其中BC段是双曲线y=$\frac{k}{x}$的一部分.请根据图中信息解答下列问题:
某蔬菜生产基地在气温较低时,用装有恒温系统的大棚栽培一种在自然光照且温度为18℃的条件下生长最快的新品种,下图是某天恒温系统从开启到关闭及关闭后,大棚内温度y(℃)随时间x(小时)变化的函数图象,其中BC段是双曲线y=$\frac{k}{x}$的一部分.请根据图中信息解答下列问题: