��Ŀ����
12��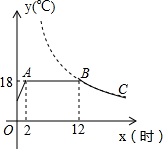 ij�߲��������������½ϵ�ʱ����װ�к���ϵͳ�Ĵ�������һ������Ȼ�������¶�Ϊ18�������������������Ʒ�֣���ͼ��ij�����ϵͳ�ӿ������رռ��رպ������¶�y���棩��ʱ��x��Сʱ���仯�ĺ���ͼ������BC����˫����y=$\frac{k}{x}$��һ���֣������ͼ����Ϣ����������⣺
ij�߲��������������½ϵ�ʱ����װ�к���ϵͳ�Ĵ�������һ������Ȼ�������¶�Ϊ18�������������������Ʒ�֣���ͼ��ij�����ϵͳ�ӿ������رռ��رպ������¶�y���棩��ʱ��x��Сʱ���仯�ĺ���ͼ������BC����˫����y=$\frac{k}{x}$��һ���֣������ͼ����Ϣ����������⣺��1������ϵͳ�����챣�ִ������¶�18���ʱ���ж���Сʱ��
��2����k��ֵ��
��3����x=18ʱ�������ڵ��¶�ԼΪ���ٶȣ�
���� ��1��ֱ������ͼ��ó�����ϵͳ�����챣�ִ������¶�18���ʱ�䣻
��2������12��18���������k��ֵ���ɣ�
��3����x=18ʱ�����y=12�����ɵó��𰸣�
��� �⣺��1������ϵͳ�����챣�ִ����¶�18���ʱ��Ϊ10Сʱ��
��2���ߵ�B��12��18����˫����y=$\frac{k}{x}$�ϣ�
��18=$\frac{k}{12}$��
��ã�k=216��
��3����x=18ʱ��y=12��
���Ե�x=18ʱ�������ڵ��¶�ԼΪ12�森
���� ������Ҫ�����˷�����������Ӧ�ã���ȷ����ͼ��ó���������ǽ���ؼ���

��ϰ��ϵ�д�
�����Ŀ
2�����и����У���-3С�����ǣ�������
| A�� | 4 | B�� | -4 | C�� | -2 | D�� | 0 |
20����֪��x1��x2��һԪ���η���x2+2ax+b=0����������x1+x2=4��x1x2=1����a��b��ֵ�ֱ��ǣ�������
| A�� | a=-4��b=1 | B�� | a=4��b=1 | C�� | a=-2��b=1 | D�� | a=-2��b=-1 |
17����֪һ�κ���y=$\frac{3}{2}$x+b�뷴��������y=$\frac{3}{x}$�У�x��y�Ķ�Ӧֵ���±���
��ʽ$\frac{3}{2}$x+b��$\frac{3}{x}$�Ľ�Ϊ��������
| x | -3 | -2 | -1 | 1 | 2 | 3 |
| y=$\frac{3}{2}$x+b | -3 | -$\frac{3}{2}$ | 0 | 3 | $\frac{9}{2}$ | 6 |
| y=$\frac{3}{x}$ | -1 | -$\frac{3}{2}$ | -3 | 3 | $\frac{3}{2}$ | 1 |
| A�� | x��-2��0��x��1 | B�� | x��1 ��-2��x��0 | C�� | -2��x��1 | D�� | x��1 ��x��-2 |
1���ں���y=$\frac{12}{x}$ͼ���ϵĵ��ǣ�������
| A�� | ��-2��6�� | B�� | ��-2��-6�� | C�� | ��3��-4�� | D�� | ��-3��4�� |
2��һ��Ь����һ��ʱ����������ij����Ь200˫�����ֳ���Ь�������������ʾ��
һ������Ь���ϰ�ȽϹ������ֳ����Ь�����Ҳ���ǹ���������Ь�ij�����ɵ�һ�����ݣ�������
| ����/���� | 23 | 23.5 | 24 | 24.5 | 25 | 25.5 |
| ������/˫ | 5 | 10 | 22 | 39 | 56 | 43 |
| A�� | ƽ���� | B�� | ��λ�� | C�� | ���� | D�� | ��Ȩƽ���� |