题目内容
13.如图,点O是△ABC的边AB上一点,以O为圆心,OB为半径的圆与AC相切于点D,且AD=CD,E是射线OB上一点,DF∥AB交CE于点F,若OA=4,∠A=45°.(1)求⊙O的半径.
(2)若E在OB上且BE=$\sqrt{2}$,求EF的长.
(3)若以E为圆心,EF为半径的圆⊙E与⊙O相切,试求⊙E的半径.
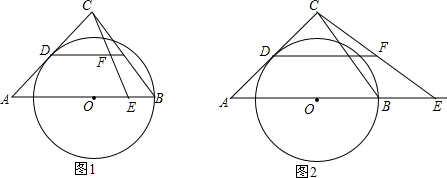
分析 (1)连接DO,易证△ADO是等腰直角三角形,利用等腰直角三角形斜边与直角边的关系求解即可;
(2)连接DO,CO,易得OD垂直平分AC,由此可得OC的值,在RT△COE中,利用勾股定理可求得EF的值;
(3)分两种情况:①当⊙E与⊙O相切于点B时,②当⊙E与⊙O相切于点M时,分别求解即可.
解答 解:(1)如图,连接DO,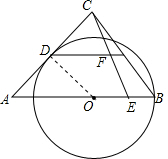
∵AC与⊙O相切于点O,
∴∠ADO=90°,
∵∠A=45°,
∴AO=$\sqrt{2}$OD,
∵OA=4,
∴OD=$\frac{4}{\sqrt{2}}$=2$\sqrt{2}$,
(2)如图1,连接DO,CO,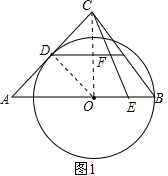
∵AC与⊙O相切于点O,
∴∠ADO=90°,
∵AD=CD,
∴OD垂直平分AC,
∴OC=AO=4,
∵DF∥AB,
∴点F为CF中点,
在RT△COE中,
∵CE=$\sqrt{C{O}^{2}+O{E}^{2}}$=$\sqrt{{4}^{2}+2}$=3$\sqrt{2}$,
∴EF=$\frac{1}{2}$CE=$\frac{3\sqrt{2}}{2}$,
(3)①如图2,当⊙E与⊙O相切于点B时,连接CO,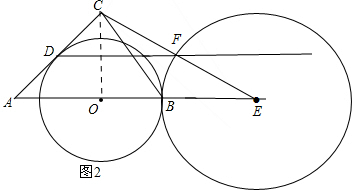
在RT△COE中,
∵CE2=CO2+OE2,
∴EF=$\frac{1}{2}$CE=$\frac{1}{2}$×$\sqrt{{4}^{2}+(2\sqrt{2}+EF)^{2}}$,解得EF=$\frac{2\sqrt{2}+4\sqrt{5}}{3}$,EF=$\frac{2\sqrt{2}-4\sqrt{5}}{3}$(舍去),
②如图3,当⊙E与⊙O相切于点M时,连接CO,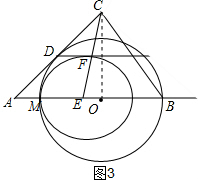
在RT△COE中,
∵CE2=CO2+OE2,
∴2EF=CE=$\sqrt{{4}^{2}+(2\sqrt{2}-EF)^{2}}$,解得EF=$\frac{2\sqrt{2}+4\sqrt{5}}{3}$(舍去),EF=$\frac{4\sqrt{5}-2\sqrt{2}}{3}$,
综上所述:⊙E的半径为:$\frac{2\sqrt{2}+4\sqrt{5}}{3}$或$\frac{4\sqrt{5}-2\sqrt{2}}{3}$.
点评 本题主要考查了圆的综合题,涉及切线定理,三角形的中位线,两圆相切及中垂线定理等知识,解题的关键是正确作出辅助线,分类讨论.

 优生乐园系列答案
优生乐园系列答案| A. | 2:3:4:5 | B. | 2:2:3:3 | C. | 2:3:2:3 | D. | 2:3:3:2 |
| A. | 4 | B. | -4 | C. | -2 | D. | 0 |