题目内容
17.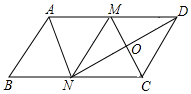 如图,在?ABCD中,M,N分别是AD,BC的中点,∠AND=90°,连接CM交DN于点O.
如图,在?ABCD中,M,N分别是AD,BC的中点,∠AND=90°,连接CM交DN于点O.(1)求证:△ABN≌△CDM;
(2)连接MN,求证四边形MNCD是菱形.
分析 (1)由四边形ABCD是平行四边形,可得AB=CD,AD=BC,∠B=∠CDM,又由M、N分别是AD,BC的中点,即可利用SAS证得△ABN≌△CDM;
(2)利用直角三角形形的性质结合菱形的判定方法证明即可.
解答 解:
(1)证明:∵四边形ABCD是平行四边形,
∴AB=CD,AD=BC,∠B=∠CDM,
∵M、N分别是AD,BC的中点,
∴BN=DM,
∵在△ABN和△CDM中,
$\left\{\begin{array}{l}{AB=CD}\\{∠B=∠CDM}\\{BN=DM}\end{array}\right.$,
∴△ABN≌△CDM(SAS);
(2)证明:
∵M是AD的中点,∠AND=90°,
∴NM=AM=MD,
∵BN=NC=AM=DM,
∴NC=MN=DM,
∵NC$\stackrel{∥}{=}$DM,
∴四边形CDMN是平行四边形,
又∵MN=DM,
∴四边形CDMN是菱形.
点评 此题主要考查了平行四边形的性质以及全等三角形的判定与性质、菱形的判定等知识,正确应用直角三角形的性质是解题关键.

练习册系列答案
 名题金卷系列答案
名题金卷系列答案
相关题目
6.已知A(x1,y1),B(x2,y2)是反比例函数y=-$\frac{{k}^{2}}{x}$图象上的两个点,且x1<x2,则y1与y2的大小关系是( )
| A. | y1<y2 | B. | y1=y2 | C. | y1>y2 | D. | 大小不确定 |
7.下列运算正确的有( )
| A. | 5ab-ab=4 | B. | 3$\sqrt{2}$-$\sqrt{2}$=3 | C. | a6÷a3=a3 | D. | $\frac{1}{a}$+$\frac{1}{b}$=$\frac{2}{a+b}$ |
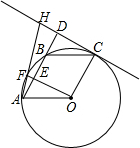 如图A、F、B、C是半圆O上的四个点,四边形OABC是平行四边形,∠FAB=15°,连接OF交AB于点E,过点C作OF的平行线交AB的延长线于点D,延长AF交直线CD于点H.
如图A、F、B、C是半圆O上的四个点,四边形OABC是平行四边形,∠FAB=15°,连接OF交AB于点E,过点C作OF的平行线交AB的延长线于点D,延长AF交直线CD于点H.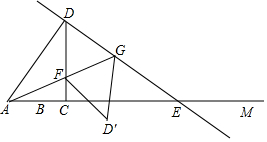 如图,射线AM上有一点B,AB=6,点C是射线AM上异于B的一点,过C作CD⊥AM,且CD=$\frac{4}{3}$AC,过D点作DE⊥AD,交射线AM于E,在射线CD取点F,使得CF=CB,连接AF并延长,交DE于点G,设AC=3x.
如图,射线AM上有一点B,AB=6,点C是射线AM上异于B的一点,过C作CD⊥AM,且CD=$\frac{4}{3}$AC,过D点作DE⊥AD,交射线AM于E,在射线CD取点F,使得CF=CB,连接AF并延长,交DE于点G,设AC=3x.