题目内容
将矩形ABCD折叠，使得对角线的两个端点A、C重合，折痕所在的直线交射线AB于点E，如果AB=3，BE=1，则BC的长是 ．
考点：翻折变换（折叠问题）
专题：
分析：分类讨论：当点E在AB上时，连结EC，根据折叠性质得EC=EA=2，再根据勾股定理可计算出BC；当点E在AB上时，连结EC，根据折叠性质得EC=EA=4，再根据勾股定理可计算出BC．
解答：解：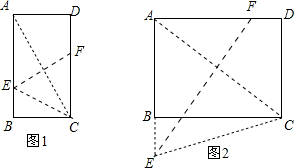
当点E在AB上时，连结EC，如图1，
AB=3，BE=1，则AE=AB-BE=2，
∵矩形ABCD折叠，使得对角线的两个端点A，C重合，折痕所在直线交直线AB与点E，
∴EC=EA=2，
在Rt△BEC中，BC=
=
，
当点E在AB上时，连结EC，如图2，
AB=3，BE=1，则AE=AB+BE=4，
∵矩形ABCD折叠，使得对角线的两个端点A，C重合，折痕所在直线交直线AB与点E，
∴EC=EA=4，
在Rt△BEC中，BC=
=
，
故答案为：
或
．
当点E在AB上时，连结EC，如图1，AB=3，BE=1，则AE=AB-BE=2，
∵矩形ABCD折叠，使得对角线的两个端点A，C重合，折痕所在直线交直线AB与点E，
∴EC=EA=2，
在Rt△BEC中，BC=
| EC2-BE2 |
| 3 |
当点E在AB上时，连结EC，如图2，
AB=3，BE=1，则AE=AB+BE=4，
∵矩形ABCD折叠，使得对角线的两个端点A，C重合，折痕所在直线交直线AB与点E，
∴EC=EA=4，
在Rt△BEC中，BC=
| EC2+BE2 |
| 17 |
故答案为：
| 3 |
| 17 |
点评：本题考查了折叠的性质：折叠是一种对称变换，它属于轴对称，折叠前后图形的形状和大小不变，位置变化，对应边和对应角相等．也考查了勾股定理、锐角三角函数以及分类讨论思想的运用．
练习册系列答案
相关题目
已知D为等边△ABC的边BC上的一点，将△ABC的上部分向下折叠，折痕为MN，M、N分别在AB、AC边上，点A落在点D处，若BD：DC=2：3，则AM：AN=
如图，是将一张长方形纸片折叠后的图形，如果∠1=100°，那么∠2=
在平面直角坐标系中，抛物线y=x2+x-1与x轴的交点的个数是（ ）
| A、3 | B、2 | C、1 | D、0 |
在代数式
、
、
、
中，是分式的有（ ）
| 1 |
| x |
| xy-y |
| 3xy |
| a+b |
| 5 |
| x+y |
| π |
| A、1个 | B、2个 | C、3个 | D、4个 |
下列各式：①
，②
，③
，④
，其中是分式的有（ ）
| 1 |
| a |
| x |
| 1+π |
| x-1 |
| 5 |
| 2 |
| 2x+y |
| A、①②③④ | B、①④ |
| C、①②④ | D、②④ |