如图.在△ABC中.AB=AC.BD平分∠ABC交AC于点D.AE∥BD交CB的延长线于点E．若∠E=35°.则∠BAC的度数为( )A．40°B．45°C．60°D．70° 题目和参考答案——青夏教育精英家教网—

题目内容

17．

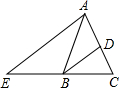如图，在△ABC中，AB=AC，BD平分∠ABC交AC于点D，AE∥BD交CB的延长线于点E．若∠E=35°，则∠BAC的度数为（　　）

A．

40°

B．

45°

C．

60°

D．

70°

分析根据平行线的性质可得∠CBD的度数，根据角平分线的性质可得∠CBA的度数，根据等腰三角形的性质可得∠C的度数，根据三角形内角和定理可得∠BAC的度数．

解答解：∵AE∥BD，
∴∠CBD=∠E=35°，
∵BD平分∠ABC，
∴∠CBA=70°，
∵AB=AC，
∴∠C=∠CBA=70°，
∴∠BAC=180°-70°×2=40°．
故选：A．

点评考查了平行线的性质，角平分线的性质，等腰三角形的性质和三角形内角和定理．关键是得到∠C=∠CBA=70°．

练习册系列答案

8．

尺规作图：已知：∠ABC，以BA为一边，在∠ABC的外部，作∠ABD，使∠ABD=2∠ABC．（要求：要保留作图痕迹）

5．阅读资料：
如图1，在平面之间坐标系xOy中，A，B两点的坐标分别为A（x₁，y₁），B（x₂，y₂），由勾股定理得AB²=|x₂-x₁|²+|y₂-y₁|²，所以A，B两点间的距离为AB=$\sqrt{（{x}_{2}-{x}_{1}）^{2}+（{y}_{2}-{y}_{1}）^{2}}$．
我们知道，圆可以看成到圆心距离等于半径的点的集合，如图2，在平面直角坐标系xoy中，A（x，y）为圆上任意一点，则A到原点的距离的平方为OA²=|x-0|²+|y-0|²，当⊙O的半径为r时，⊙O的方程可写为：x²+y²=r²．
问题拓展：如果圆心坐标为P（a，b），半径为r，那么⊙P的方程可以写为（x-a）²+（y-b）²=r²．
综合应用：
如图3，⊙P与x轴相切于原点O，P点坐标为（0，6），A是⊙P上一点，连接OA，使tan∠POA=$\frac{3}{4}$，作PD⊥OA，垂足为D，延长PD交x轴于点B，连接AB．
①证明AB是⊙P的切线；
②是否存在到四点O，P，A，B距离都相等的点Q？若存在，求Q点坐标，并写出以Q为圆心，以OQ为半径的⊙Q的方程；若不存在，说明理由．

12．等腰三角形边长分别为a，b，2，且a，b是关于x的一元二次方程x²-6x+n-1=0的两根，则n的值为
（　　）

2．已知实数a，b满足：a²+1=$\frac{1}{a}$，b²+1=$\frac{1}{b}$，则2015^|a-b|=1．

9．（1）计算：|-5|+$\sqrt{4}$×2^-1；
（2）化简：a（2-a）+（a+1）（a-1）．

6．若∠A=34°，则∠A的补角为（　　）

7．沅江市近年来大力发展芦笋产业，某芦笋生产企业在两年内的销售额从20万元增加到80万元．设这两年的销售额的年平均增长率为x，根据题意可列方程为（　　）

试题分类