题目内容
14.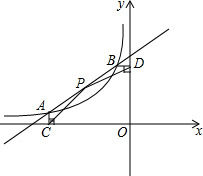 如图,A(-4,$\frac{1}{2}$),B(-1,2)是一次函数y1=ax+b与反比例函数y2=$\frac{m}{x}$图象的两个交点,AC⊥x轴于点C,BD⊥y轴于点D.
如图,A(-4,$\frac{1}{2}$),B(-1,2)是一次函数y1=ax+b与反比例函数y2=$\frac{m}{x}$图象的两个交点,AC⊥x轴于点C,BD⊥y轴于点D.(1)根据图象直接回答:在第二象限内,当x取何值时,y1-y2>0?
(2)求一次函数解析式及m的值;
(3)P是线段AB上一点,连接PC,PD,若△PCA和△PDB面积相等,求点P的坐标.
分析 (1)观察函数图象得到当-4<x<-1时,一次函数图象都在反比例函数图象上方;
(2)先利用待定系数法求一次函数解析式,然后把B点坐标代入y=$\frac{m}{x}$可计算出m的值;
(3)设P点坐标为(m,$\frac{1}{2}$m+$\frac{5}{2}$),利用三角形面积公式可得到$\frac{1}{2}$•$\frac{1}{2}$•(m+4)=$\frac{1}{2}$•1•(2-$\frac{1}{2}$m-$\frac{5}{2}$),解方程得到m=-$\frac{5}{2}$,从而可确定P点坐标.
解答 解:(1)当y1-y2>0,
即:y1>y2,
∴一次函数y1=ax+b的图象在反比例函数y2=$\frac{m}{x}$图象的上面,
∵A(-4,$\frac{1}{2}$),B(-1,2)
∴当-4<x<-1时,y1-y2>0;
(2)∵y2=$\frac{m}{x}$图象过B(-1,2),
∴m=-1×2=-2,
∵y1=ax+b过A(-4,$\frac{1}{2}$),B(-1,2),
∴$\left\{\begin{array}{l}{-4a+b=\frac{1}{2}}\\{-a+b=2}\end{array}\right.$,解得$\left\{\begin{array}{l}{a=\frac{1}{2}}\\{b=\frac{5}{2}}\end{array}\right.$,
∴一次函数解析式为;y=$\frac{1}{2}$x+$\frac{5}{2}$,
(3)设P(m,$\frac{1}{2}$m+$\frac{5}{2}$),过P作PM⊥x轴于M,PN⊥y轴于N,
∴PM=$\frac{1}{2}$m+$\frac{5}{2}$,PN=-m,
∵△PCA和△PDB面积相等,
∴$\frac{1}{2}AC•CM=\frac{1}{2}$BD•DN,
即;$\frac{1}{2}×\frac{1}{2}(m+4)=\frac{1}{2}×1×(2-\frac{1}{2}m-\frac{5}{2})$,
解得m=-$\frac{5}{2}$,
∴P(-$\frac{5}{2}$,$\frac{5}{4}$).
点评 本题考查了反比例函数与一次函数的交点问题:反比例函数与一次函数图象的交点坐标满足两函数解析式.也考查了待定系数法求函数解析式以及观察函数图象的能力.

| A. | $\frac{120}{x+2}$+3=$\frac{120}{x}$ | B. | $\frac{120}{x}$=$\frac{120}{x+2}$-3 | C. | $\frac{120}{x-2}$=$\frac{120}{x}$+3 | D. | $\frac{120}{x-2}$=$\frac{120}{x}$-3 |
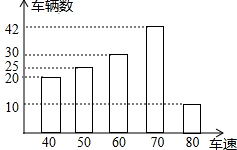 为了了解一路段车辆行驶速度的情况,交警统计了该路段上午7::0至9:00来往车辆的车速(单位:千米/时),并绘制成如图所示的条形统计图.这些车速的众数、中位数分别是( )
为了了解一路段车辆行驶速度的情况,交警统计了该路段上午7::0至9:00来往车辆的车速(单位:千米/时),并绘制成如图所示的条形统计图.这些车速的众数、中位数分别是( )| A. | 众数是80千米/时,中位数是60千米/时 | |
| B. | 众数是70千米/时,中位数是70千米/时 | |
| C. | 众数是60千米/时,中位数是60千米/时 | |
| D. | 众数是70千米/时,中位数是60千米/时 |
| A. | 56° | B. | 146° | C. | 156° | D. | 166° |
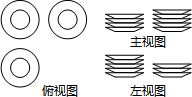 一张桌子上摆放有若干个大小、形状完全相同的碟子,现从三个方向看,其三种视图如图所示,则这张桌子上碟子的总数为( )
一张桌子上摆放有若干个大小、形状完全相同的碟子,现从三个方向看,其三种视图如图所示,则这张桌子上碟子的总数为( )| A. | 11 | B. | 12 | C. | 13 | D. | 14 |

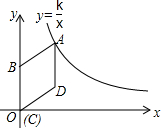 如图,在平面直角坐标系中,菱形ABCD的顶点C与原点O重合,点B在y轴的正半轴上,点A在反比例函数y=$\frac{k}{x}$(k>0,x>0)的图象上,点D的坐标为(4,3).
如图,在平面直角坐标系中,菱形ABCD的顶点C与原点O重合,点B在y轴的正半轴上,点A在反比例函数y=$\frac{k}{x}$(k>0,x>0)的图象上,点D的坐标为(4,3).