题目内容
解下列不等式(组)
(1)3(x+1)<4(x-2)-3;
(2)
.
(1)3(x+1)<4(x-2)-3;
(2)
|
考点:解一元一次不等式组,解一元一次不等式
专题:
分析:(1)首先去括号,然后移项、合并同类项,系数化成1即可求解;
(2)先求出不等式组中每一个不等式的解集,再求出它们的公共部分,就是不等式组的解集.
(2)先求出不等式组中每一个不等式的解集,再求出它们的公共部分,就是不等式组的解集.
解答:解:(1)去括号,得:3x+3<4x-8-3,
移项,得:3x-4x<-8-3-3,
合并同类项,得:-x<-14,
系数化成1得:x>14;
(2)
,
解①得:x<1,
解②得:x≤-2,
则不等式组的解集是:x≤-2.
移项,得:3x-4x<-8-3-3,
合并同类项,得:-x<-14,
系数化成1得:x>14;
(2)
|
解①得:x<1,
解②得:x≤-2,
则不等式组的解集是:x≤-2.
点评:本题考查的是一元一次不等式组的解,解此类题目常常要结合数轴来判断.还可以观察不等式的解,若x>较小的数、<较大的数,那么解集为x介于两数之间.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
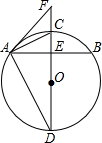 如图,已知CD为⊙O的直径,弦AB⊥CD,垂足为E,连接AD、AC,点F在DC延长线上,连接AF,且∠FAC=∠CAB.
如图,已知CD为⊙O的直径,弦AB⊥CD,垂足为E,连接AD、AC,点F在DC延长线上,连接AF,且∠FAC=∠CAB.
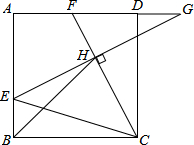 如图,在边长为6
如图,在边长为6 如图,有一矩形纸片ABCD,AB=8,AD=17,将此矩形纸片折叠,使顶点A落在BC边的A′处,折痕所在直线同时经过边AB、AD(包括端点),设BA′=x,则x的取值范围是
如图,有一矩形纸片ABCD,AB=8,AD=17,将此矩形纸片折叠,使顶点A落在BC边的A′处,折痕所在直线同时经过边AB、AD(包括端点),设BA′=x,则x的取值范围是