题目内容
 如图,有一矩形纸片ABCD,AB=8,AD=17,将此矩形纸片折叠,使顶点A落在BC边的A′处,折痕所在直线同时经过边AB、AD(包括端点),设BA′=x,则x的取值范围是
如图,有一矩形纸片ABCD,AB=8,AD=17,将此矩形纸片折叠,使顶点A落在BC边的A′处,折痕所在直线同时经过边AB、AD(包括端点),设BA′=x,则x的取值范围是考点:翻折变换(折叠问题),勾股定理
专题:几何图形问题
分析:作出图形,根据矩形的对边相等可得BC=AD,CD=AB,当折痕经过点D时,根据翻折的性质可得A′D=AD,利用勾股定理列式求出A′C,再求出BA′;当折痕经过点B时,根据翻折的性质可得BA′=AB,此两种情况为BA′的最小值与最大值的情况,然后写出x的取值范围即可.
解答: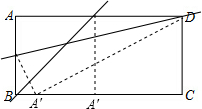 解:如图,∵四边形ABCD是矩形,AB=8,AD=17,
解:如图,∵四边形ABCD是矩形,AB=8,AD=17,
∴BC=AD=17,CD=AB=8,
①当折痕经过点D时,
由翻折的性质得,A′D=AD=17,
在Rt△A′CD中,A′C=
=
=15,
∴BA′=BC-A′C=17-15=2;
②当折痕经过点B时,由翻折的性质得,BA′=AB=8,
∴x的取值范围是2≤x≤8.
故答案为:2≤x≤8.
 解:如图,∵四边形ABCD是矩形,AB=8,AD=17,
解:如图,∵四边形ABCD是矩形,AB=8,AD=17,∴BC=AD=17,CD=AB=8,
①当折痕经过点D时,
由翻折的性质得,A′D=AD=17,
在Rt△A′CD中,A′C=
| A′D2-CD2 |
| 172-82 |
∴BA′=BC-A′C=17-15=2;
②当折痕经过点B时,由翻折的性质得,BA′=AB=8,
∴x的取值范围是2≤x≤8.
故答案为:2≤x≤8.
点评:本题考查了翻折变换的性质,勾股定理的应用,难点在于判断出BA′的最小值与最大值时的情况,作出图形更形象直观.

练习册系列答案
 名题金卷系列答案
名题金卷系列答案
相关题目
下列现象:①电梯的升降运动,②飞机在地面上沿直线滑行,③风车的转动,④冷水加热过程中气泡的上升.其中属于平移的是( )
| A、①② | B、①③ | C、②③ | D、③④ |
 如图,在⊙O中,CD是直径,弦AB⊥CD,垂足为E,连接BC,若AB=2
如图,在⊙O中,CD是直径,弦AB⊥CD,垂足为E,连接BC,若AB=2
 如图,BE=CF中,AF=DE,△ABF≌△DCE两点分别在边ABCD上,且DE与BC不平行.请填上一个你认为合适的条件:
如图,BE=CF中,AF=DE,△ABF≌△DCE两点分别在边ABCD上,且DE与BC不平行.请填上一个你认为合适的条件: 如图,在平面直角坐标系中,BO=5,CB=2
如图,在平面直角坐标系中,BO=5,CB=2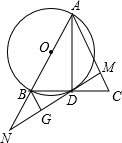 如图,已知在△ABC中,AD是BC边上的中线,以AB为直径的⊙O交BC于点D,过D作MN⊥AC于点M,交AB的延长线于点N,过点B作BG⊥MN于G.
如图,已知在△ABC中,AD是BC边上的中线,以AB为直径的⊙O交BC于点D,过D作MN⊥AC于点M,交AB的延长线于点N,过点B作BG⊥MN于G.