题目内容
1. 如图所示,在△ABC中,已知点D,E,F分别是AC、BD,CE的中点,且S△ABC=6平方厘米,则S△AEF的值为1.5平方厘米.
如图所示,在△ABC中,已知点D,E,F分别是AC、BD,CE的中点,且S△ABC=6平方厘米,则S△AEF的值为1.5平方厘米.
分析 根据等底等高的三角形的面积相等可知,三角形的中线把三角形分成面积相等的两个三角形,然后求解即可.
解答 解:∵D是AC的中点,
∴S△BAD=S△BCD=$\frac{1}{2}$S△ABC=$\frac{1}{2}$×6=3cm2,
∵E是BD的中点,
∴S△ADE=S△CDE=$\frac{1}{2}$×3=$\frac{3}{2}$cm2,
∴S△AEF=$\frac{1}{2}$(S△ADE+S△CDE)=$\frac{1}{2}$($\frac{3}{2}$+$\frac{3}{2}$)=1.5cm2.
故答案为:1.5.
点评 本题考查了三角形的面积,熟记三角形的中线把三角形分成面积相等的两个三角形是解题的关键.

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目
12.青藏高原是世界上海拔最高的高原,它的面积约为2500000千米2,用科学记数法可表示为( )
| A. | 0.25×107千米2 | B. | 2.5×105千米2 | C. | 2.5×106千米2 | D. | 2.5×107千米2 |
13.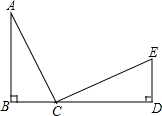 如图,已知AB⊥BD,ED⊥BD,AB=CD,AC=CE,则∠ACE等于( )
如图,已知AB⊥BD,ED⊥BD,AB=CD,AC=CE,则∠ACE等于( )
 如图,已知AB⊥BD,ED⊥BD,AB=CD,AC=CE,则∠ACE等于( )
如图,已知AB⊥BD,ED⊥BD,AB=CD,AC=CE,则∠ACE等于( )| A. | 90° | B. | 120° | C. | 80° | D. | 100° |
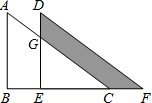 如图是重叠的两个直角三角形,将其中一个直角三角形沿BC方向平移得到三角形DEF,若AB=8cm,BE=4cm,DG=3cm,则图中阴影部分的面积是多少cm2?
如图是重叠的两个直角三角形,将其中一个直角三角形沿BC方向平移得到三角形DEF,若AB=8cm,BE=4cm,DG=3cm,则图中阴影部分的面积是多少cm2? 如图所示,利用面积的不同表示方法可证明(a+b)(a-b)=a2-b2,你能说明其中的道理吗?
如图所示,利用面积的不同表示方法可证明(a+b)(a-b)=a2-b2,你能说明其中的道理吗?