题目内容
13.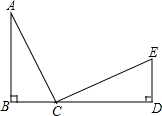 如图,已知AB⊥BD,ED⊥BD,AB=CD,AC=CE,则∠ACE等于( )
如图,已知AB⊥BD,ED⊥BD,AB=CD,AC=CE,则∠ACE等于( )| A. | 90° | B. | 120° | C. | 80° | D. | 100° |
分析 由题中条件可得Rt△ABC≌Rt△CDE,再通过角之间的转化,进而可得出结论.
解答 解:∵AB⊥BD,ED⊥BD,
∴∠D=∠B=90°,
在Rt△ABC和Rt△CDE中,
$\left\{\begin{array}{l}{AB=CD}\\{AC=CE}\end{array}\right.$,
∴Rt△ABC≌Rt△CDE(HL),
∴∠DCE=∠A,
∵∠B=90°,
∴∠BAC+∠ACB=90°,
∴∠ECD+∠ACB=90°,
∴∠ACE=180°-90°=90°.
故选:A.
点评 本题主要考查了全等三角形的判定及性质,解决本题的关键是证明Rt△ABC≌Rt△CDE.

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案
相关题目
5.数1、0、$\frac{1}{2}$、-3、$-\frac{1}{5}$可以统称为( )
| A. | 整数 | B. | 分数 | C. | 负数 | D. | 有理数 |
 如图所示,在△ABC中,已知点D,E,F分别是AC、BD,CE的中点,且S△ABC=6平方厘米,则S△AEF的值为1.5平方厘米.
如图所示,在△ABC中,已知点D,E,F分别是AC、BD,CE的中点,且S△ABC=6平方厘米,则S△AEF的值为1.5平方厘米.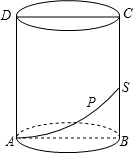 如图,在圆柱的截面ABCD中,AB=$\frac{16}{π}$,BC=12,动点P从A点出发,沿着圆柱的侧面移动到BC的中点S的最短距离为10.
如图,在圆柱的截面ABCD中,AB=$\frac{16}{π}$,BC=12,动点P从A点出发,沿着圆柱的侧面移动到BC的中点S的最短距离为10. 如图,数轴上点A对应一个有理数,那么与A点相距3个单位长度的点所对应的有理数是-5或1.
如图,数轴上点A对应一个有理数,那么与A点相距3个单位长度的点所对应的有理数是-5或1.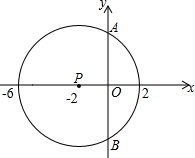 如图,已知⊙P的圆心为P(-2,0),与x轴有公共点(-6,0),(2,0).
如图,已知⊙P的圆心为P(-2,0),与x轴有公共点(-6,0),(2,0).