题目内容
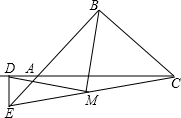 已知在Rt△ABC中,AB=BC.在Rt△ADE中,AD=DE;连接EC,取EC中点M,连接DM和BM.点D在CA的延长线上,点E在BA的延长线上,求证:BM=DM,BM⊥DM.
已知在Rt△ABC中,AB=BC.在Rt△ADE中,AD=DE;连接EC,取EC中点M,连接DM和BM.点D在CA的延长线上,点E在BA的延长线上,求证:BM=DM,BM⊥DM.考点:全等三角形的判定与性质
专题:
分析:根据直角三角形斜边上中线性质得出BM=MC=ME,DM=EM=MC,推出BM=DM,∠3=∠MDC,∠6=∠4,求出∠1+∠2=90°,求出∠DMB=90°,即可得出答案.
解答:证明:∵在Rt△EBC和△EDC中,M为EC的中点,
∴BM=MC=ME,DM=EM=MC,
∴BM=DM,∠3=∠MDC,∠6=∠4,
∵∠1=∠6+∠4=2∠6,∠2=∠MDC+∠3=2∠3,
∵∠DAE=∠3+∠6=45°,
∴∠1+∠2=90°,
∴∠DMB=180°-90°=90°,
∴DM⊥BM.

∴BM=MC=ME,DM=EM=MC,
∴BM=DM,∠3=∠MDC,∠6=∠4,
∵∠1=∠6+∠4=2∠6,∠2=∠MDC+∠3=2∠3,
∵∠DAE=∠3+∠6=45°,
∴∠1+∠2=90°,
∴∠DMB=180°-90°=90°,
∴DM⊥BM.
点评:此题考查了直角三角形的斜边上中线性质,等腰三角形的性质的应用,主要考查学生综合运用性质进行推理的能力,有一定的难度.

练习册系列答案
相关题目
设⊙O的半径为r,圆心O到直线l的距离为d,关于x的方程r2(x2+1)-2d2x=0有两个相等的实数根,则直线l与⊙O( )
| A、相离 | B、相切 |
| C、相交 | D、相切或相交 |
 如图,在等边△ABC中,BC=8,D为AB中点,点E在BC上,点F在AC上,满足AF=3CF,DE平分∠BDF,则BE=
如图,在等边△ABC中,BC=8,D为AB中点,点E在BC上,点F在AC上,满足AF=3CF,DE平分∠BDF,则BE= 如图,菱形ABCD的周长为40cm,它的一条对角线BD长10cm.
如图,菱形ABCD的周长为40cm,它的一条对角线BD长10cm.