题目内容
已知抛物线y=x2+bx+c与x轴交于A（1，0）、B（3，0），则当y＜0时对应的x的取值范围是 ．
考点：抛物线与x轴的交点
专题：
分析：先根据抛物线y=x2+bx+c可知开口向上，然后根据和x轴交点的横坐标，即可求出y＜0时，x的取值范围．
解答：解：抛物线y=x2+bx+c与x轴的交点的横坐标分别为A（1，0）、B（3，0），
∴抛物线开口向上，
∴当y＜0时，x的取值范围正好在两交点之间，即1＜x＜3．
故答案为1＜x＜3．
∴抛物线开口向上，
∴当y＜0时，x的取值范围正好在两交点之间，即1＜x＜3．
故答案为1＜x＜3．
点评：本题考查了抛物线和x轴的交点，根据开口方向判定图象所处的位置是解此题的关键．
练习册系列答案
第1卷单元月考期中期末系列答案
相关题目
若方程x2-5x-10=0的两根为x1、x2，则
+
的值为（ ）
| 1 |
| x1 |
| 1 |
| x2 |
| A、2 | ||
| B、-2 | ||
C、
| ||
D、-
|
如图，在等边△ABC中，BC=8，D为AB中点，点E在BC上，点F在AC上，满足AF=3CF，DE平分∠BDF，则BE=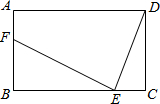
如图，在矩形ABCD中，AB=6，BC=9，E为线段BC上的动点（不与B、C重合）．连接DE，作EF⊥DE，EF与线段AB交于点F，设CE=x．