题目内容
如图,在Rt△ABC中,∠ACB=90°,CP平分∠ACB,CP与AB交于点D,且PA=PB.
①求证:△APB是等腰直角三角形;
②设PA=m,PC=n,试用m、n的代数式表示△ABC的周长;
③试探索当边AC、BC的长度变化时,
+
的值是否发生变化?若不变,请求出它的值;若变化,试说明理由.
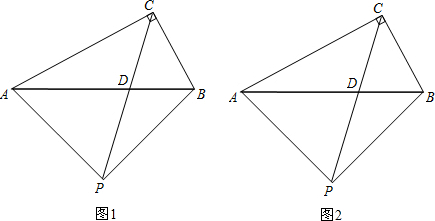
①求证:△APB是等腰直角三角形;
②设PA=m,PC=n,试用m、n的代数式表示△ABC的周长;
③试探索当边AC、BC的长度变化时,
| DC |
| AC |
| DC |
| BC |

考点:相似三角形的判定与性质,全等三角形的判定与性质,角平分线的性质,等腰直角三角形
专题:
分析:(1)过P作PEPE⊥AC,PF⊥BC,垂足分别是E、F,易证四边形PECF为正方形,进一步可证得Rt△APE≌Rt△BPF,可得出结论;
(2)利用勾股定理求得AB,利用(1)可得出AE=BF,从而可表示出△ABC的周长为2CE,再用n表示出CE即可求得其周长;
(3)利用△ADC≌△PDB、△ADP≌△CDB,代入计算,
+
即可.
(2)利用勾股定理求得AB,利用(1)可得出AE=BF,从而可表示出△ABC的周长为2CE,再用n表示出CE即可求得其周长;
(3)利用△ADC≌△PDB、△ADP≌△CDB,代入计算,
| DC |
| AC |
| DC |
| BC |
解答:(1)证明:如图,过P作PE⊥AC,PF⊥BC,垂足分别是E、F,
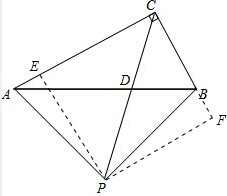
∴∠PEC=∠PFC=∠ECF=90°,
∴四边形PECF为矩形,
∵PC平分∠ACB,
∴∠PCE=45°,
∴PE=EC,
∴四边形PECF为正方形,
∴EP=FP,∠EPF=90°,
在Rt△APE和Rt△BPF中,
,
∴Rt△APE≌Rt△BPF(HL),
∴∠EPA=∠FPB,
∴∠APB=90°,
∴△APB是等腰直角三角形;
(2)解:∵PA=m,
∴AB=
m,
由Rt△APE≌Rt△BPF可得AE=BF,
∴AC+BC=AE+EC+BC=EC+CF=2EC=2nsin45°=
n,
∴△ABC的周长=
m+
n;
(3)解:不变,理由如下:
由上可得△ADC≌△PDB、△ADP≌△CDB,
∴
=
,
=
,
∴
=
,
=
,
∵AP=PB,
∴
+
=
=
.

∴∠PEC=∠PFC=∠ECF=90°,
∴四边形PECF为矩形,
∵PC平分∠ACB,
∴∠PCE=45°,
∴PE=EC,
∴四边形PECF为正方形,
∴EP=FP,∠EPF=90°,
在Rt△APE和Rt△BPF中,
|
∴Rt△APE≌Rt△BPF(HL),
∴∠EPA=∠FPB,
∴∠APB=90°,
∴△APB是等腰直角三角形;
(2)解:∵PA=m,
∴AB=
| 2 |
由Rt△APE≌Rt△BPF可得AE=BF,
∴AC+BC=AE+EC+BC=EC+CF=2EC=2nsin45°=
| 2 |
∴△ABC的周长=
| 2 |
| 2 |
(3)解:不变,理由如下:
由上可得△ADC≌△PDB、△ADP≌△CDB,
∴
| DC |
| DB |
| AC |
| PB |
| DC |
| AD |
| BC |
| AP |
∴
| DC |
| AC |
| DB |
| PB |
| DC |
| BC |
| AD |
| AP |
∵AP=PB,
∴
| DC |
| AC |
| DC |
| BC |
| AB |
| AP |
| 2 |
点评:本题主要考查全等三角形的判定和性质及正方形的判定和性质、等腰直角三角形的判定等,构造三角形全等是解题的关键.

练习册系列答案
相关题目
如果3x2myn与-5x4y3是同类项,则m和n的取值是( )
| A、3和-2 | B、-3和2 |
| C、2和3 | D、-3和-2 |
下列计算中,正确的是( )
| A、2a+3b=5ab |
| B、a•a3=a3 |
| C、a6-a5=a |
| D、(-ab)2=a2b2 |
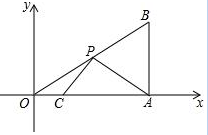 如图,Rt△OAB的直角顶点A在x轴的正半轴上,∠AOB=30°,B(6,
如图,Rt△OAB的直角顶点A在x轴的正半轴上,∠AOB=30°,B(6,