题目内容
在△ABC中,∠C=90°,a,b,c分别是∠A,∠B,∠C的对边.
(1)求证:0<sinA<1;
(2)求证:sinA+sinB>1.
(1)求证:0<sinA<1;
(2)求证:sinA+sinB>1.
考点:解直角三角形
专题:证明题
分析:(1)运用正弦函数的定义表示出sinA,即可解决问题.
(2)表示出sinA+sinB=
+
,运用三角形的三边关系,即可解决问题.
(2)表示出sinA+sinB=
| a |
| c |
| b |
| c |
解答:解:(1)由正弦函数的定义得:sinA=
,
∵0<a<c,
∴0<sinA<1.
(2)∵sinA+sinB=
+
=
,而a+b>c,
∴sinA+sinB>1.
| a |
| c |
∵0<a<c,
∴0<sinA<1.
(2)∵sinA+sinB=
| a |
| c |
| b |
| c |
=
| a+b |
| c |
∴sinA+sinB>1.
点评:该题主要考查了解直角三角形中的函数问题;解题的关键是正确运用三角函数的定义,来分析、判断、解答.

练习册系列答案
相关题目
 如图所示的立方体,如果把它展开,可以是下列图形中的( )
如图所示的立方体,如果把它展开,可以是下列图形中的( )A、 |
B、 |
C、 |
D、 |
 已知:如图,在△ABC中,AD为中线,E在AB上,AE=AC,CE交AD于F,EF:FC=3:5,EB=8cm.求:AB,AC的长.
已知:如图,在△ABC中,AD为中线,E在AB上,AE=AC,CE交AD于F,EF:FC=3:5,EB=8cm.求:AB,AC的长.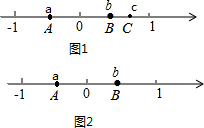 有理数a,b,c在数轴上对应的点分别为A,B,C.
有理数a,b,c在数轴上对应的点分别为A,B,C. 如图,AB、ED分别垂直于BD,点B、D是垂足,且AB=CD,AC=CE.
如图,AB、ED分别垂直于BD,点B、D是垂足,且AB=CD,AC=CE.