题目内容
某校要从甲、乙两名跳远运动员中挑选一人参加一项校际比赛．在最近10次选拔赛中，他们的成绩（单位：cm）如下：
甲：585 596 610 598 612 597 604 600 597 601
乙：613 618 580 581 618 593 585 590 598 624
（1）他们的平均成绩分别是多少？
（2）甲、乙这10次比赛成绩的方差分别是多少？
解：（1）
=
（585+596+…+601）=600，
=（613+618+…+624）=600；
（2）S2甲=[（585-600）2+（596-600）2+…+（601-600）2]=52.4，
S2乙=[（613-600）2+（618-600）2+…+（624-600）2]=253.2．
分析：（1）根据平均数的公式进行计算即可；
（2）根据方差的计算公式：S2=
[（x1-
）2+（x2-）2+…+（xn-）2]，求解即可．
点评：本题考查方差的定义：一般地设n个数据，x1，x2，…xn的平均数为，则方差S2=[（x1-）2+（x2-）2+…+（xn-）2]．
=（585+596+…+601）=600，=（613+618+…+624）=600；（2）S2甲=
[（585-600）2+（596-600）2+…+（601-600）2]=52.4，S2乙=
[（613-600）2+（618-600）2+…+（624-600）2]=253.2．分析：（1）根据平均数的公式进行计算即可；
（2）根据方差的计算公式：S2=
[（x1-）2+（x2-）2+…+（xn-）2]，求解即可．点评：本题考查方差的定义：一般地设n个数据，x1，x2，…xn的平均数为
，则方差S2=[（x1-）2+（x2-）2+…+（xn-）2]． 
练习册系列答案
阅读快车系列答案
相关题目
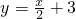交两坐标轴于A，B两点，平移抛物线
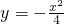，使其同时过A，B两点，求平移后的抛物线的顶点坐标．
．
；
．
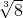如图，点C、D分别在⊙O的半径OA、OB的延长线上，且OA=3，AC=2，CD平行于AB，并与
相交于MN两点．若tan∠C=
，则弦MN的长为
