题目内容
设直线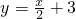
交两坐标轴于A，B两点，平移抛物线
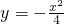，使其同时过A，B两点，求平移后的抛物线的顶点坐标．
解：∵直线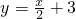交两坐标轴于A，B两点，
∴A，B两点的坐标为（-6，0），（0，3）．
设平移后抛物线的解析式为y=-
x2+bx+c，
将A，B两点的坐标代入，得
，
解得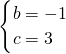
，
∴y=-x2-x+3=-（x+2）2+4，
∴顶点坐标为（-2，4）．
分析：先求出直线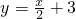与两坐标轴的交点A，B的坐标，再设平移后抛物线的解析式为y=-x2+bx+c，将A，B两点的坐标代入，得到关于b、c的方程组，解方程组求出b、c的值，得到二次函数的解析式，然后利用配方法即可求出顶点坐标．
点评：本题考查了二次函数图象与几何变换，利用待定系数法求函数的解析式，二次函数的性质，根据抛物线平移后的形状不变，得出a不变是解题的关键．
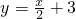交两坐标轴于A，B两点，∴A，B两点的坐标为（-6，0），（0，3）．
设平移后抛物线的解析式为y=-
x2+bx+c，将A，B两点的坐标代入，得
，解得
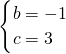，∴y=-
x2-x+3=-（x+2）2+4，∴顶点坐标为（-2，4）．
分析：先求出直线
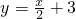与两坐标轴的交点A，B的坐标，再设平移后抛物线的解析式为y=-x2+bx+c，将A，B两点的坐标代入，得到关于b、c的方程组，解方程组求出b、c的值，得到二次函数的解析式，然后利用配方法即可求出顶点坐标．点评：本题考查了二次函数图象与几何变换，利用待定系数法求函数的解析式，二次函数的性质，根据抛物线平移后的形状不变，得出a不变是解题的关键．
练习册系列答案
相关题目
（2013•石景山区一模）如图，把两个全等的Rt△AOB和Rt△ECD分别置于平面直角坐标系xOy中，使点E与点B重合，直角边OB、BC在y轴上．已知点D （4，2），过A、D两点的直线交y轴于点F．若△ECD沿DA方向以每秒