题目内容
3. 在平行四边形ABCD中,E为AD的中点,如果AF:BF=2:5,则$\frac{AG}{GC}$=$\frac{2}{9}$.
在平行四边形ABCD中,E为AD的中点,如果AF:BF=2:5,则$\frac{AG}{GC}$=$\frac{2}{9}$.
分析 首先延长FE交CD于点H,由四边形ABCD是平行四边形,易证得△AEF∽△DEH,△AFG∽△CHG,又由E为AD的中点,AF:BF=2:5,根据相似三角形的对应边成比例,即可求得答案.
解答  解:延长FE交CD于点H,
解:延长FE交CD于点H,
∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,
∴△AEF∽△DEH,△AFG∽△CHG,
∴AE:DE=DH:AF,
∵E为AD的中点,
∴DH=AF,
∵△AFG∽△CHG,
∴AG:GC=AF:CH,
∵AF:BF=2:5,
∴AF:AB=2:7,
∴AF:CH=2:9,
∴AG:GC=2:9,
故答案为$\frac{2}{9}$.
点评 此题考查了平行四边形的性质以及相似三角形的判定与性质,注意掌握数形结合思想的应用,正确做出辅助线构造相似三角形是解题的关键.

练习册系列答案
 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
14.下面有理数中,最大的数是( )
| A. | $-\frac{1}{2}$ | B. | 0 | C. | -1 | D. | -3 |
12.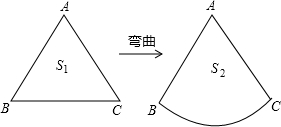 如图,△ABC为等边三角形,保持各边的长度不变,将BC边向三角形外弯曲得到扇形ABC,设△ABC的面积为S1,扇形ABC的面积为S2,则S1与S2的大小关系为( )
如图,△ABC为等边三角形,保持各边的长度不变,将BC边向三角形外弯曲得到扇形ABC,设△ABC的面积为S1,扇形ABC的面积为S2,则S1与S2的大小关系为( )
 如图,△ABC为等边三角形,保持各边的长度不变,将BC边向三角形外弯曲得到扇形ABC,设△ABC的面积为S1,扇形ABC的面积为S2,则S1与S2的大小关系为( )
如图,△ABC为等边三角形,保持各边的长度不变,将BC边向三角形外弯曲得到扇形ABC,设△ABC的面积为S1,扇形ABC的面积为S2,则S1与S2的大小关系为( )| A. | S1<S2 | B. | S1=S2 | C. | S1>S2 | D. | 无法确定 |
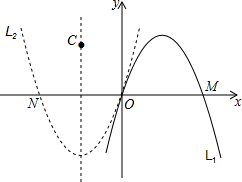 在直角坐标系xOy中,定义点C(a,b)为抛物线L:y=ax2+bx(a≠0)的特征点坐标.
在直角坐标系xOy中,定义点C(a,b)为抛物线L:y=ax2+bx(a≠0)的特征点坐标.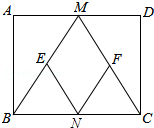 已知:如图,在矩形ABCD中,M、N分别是边AD、BC的中点,E、F分别是线段BM、CM的中点.
已知:如图,在矩形ABCD中,M、N分别是边AD、BC的中点,E、F分别是线段BM、CM的中点.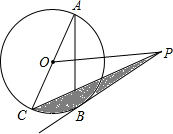 已知:如图,AC是⊙O的直径,BC是⊙O的弦,点P是⊙O外一点.∠PBA=∠ACB.
已知:如图,AC是⊙O的直径,BC是⊙O的弦,点P是⊙O外一点.∠PBA=∠ACB.