题目内容
3.学校需要购买一批篮球和足球,已知一个篮球比一个足球的进价高30元,买两个篮球和三个足球一共需要510元.(1)求篮球和足球的单价;
(2)根据实际需要,学校决定购买篮球和足球共100个,其中篮球购买的数量不少于足球数量的$\frac{2}{3}$,学校可用于购买这批篮球和足球的资金最多为10500元.请问有几种购买方案?
(3)若购买篮球x个,学校购买这批篮球和足球的总费用为y(元),在(2)的条件下,求哪种方案能使y最小,并求出y的最小值.
分析 (1)设一个篮球x元,则一个足球(x-30)元,根据“买两个篮球和三个足球一共需要510元”列出方程,即可解答;
(2)设购买篮球x个,足球(100-x)个,根据“篮球购买的数量不少于足球数量的$\frac{2}{3}$,学校可用于购买这批篮球和足球的资金最多为10500元”,列出不等式组,求出x的取值范围,由x为正整数,即可解答;
(3)表示出总费用y,利用一次函数的性质,即可确定x的取值,即可确定最小值.
解答 解:(1)设一个篮球x元,则一个足球(x-30)元,由题意得:
2x+3(x-30)=510,
解得:x=120,
∴一个篮球120元,一个足球90元.
(2)设购买篮球x个,足球(100-x)个,
由题意可得:$\left\{\begin{array}{l}{x≥\frac{2}{3}(100-x)}\\{120x+90(100-x)≤10500}\end{array}\right.$,
解得:40≤x≤50,
∵x为正整数,
∴x=40,41,42,43,44,45,46,47,48,49,50,
∴共有11种购买方案.
(3)由题意可得y=120x+90(100-x)=30x+9000(40≤x≤50)
∵k=30>0,
∴y随x的增大而增大,
∴当x=40时,y有最小值,y最小=30×40+9000=10200(元),
所以当x=40时,y最小值为10200元.
点评 本题考查了一次函数的应用,解决本题的关键是根据已知条件,列出一元一次方程和一元一次不等式组,应用一次函数的性质解决问题.

练习册系列答案
 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案
相关题目
18.若顺次连接四边形ABCD四边的中点,得到的图形是一个矩形,则四边形ABCD一定是( )
| A. | 矩形 | B. | 菱形 | ||
| C. | 对角线相等的四边形 | D. | 对角线互相垂直的四边形 |
2.某校将举行一场“汉字电脑录入大赛”,要求各班推选一名同学参加比赛.为此,初三(1)班组织了五轮班级选拔赛,在这五轮选拔赛中,甲、乙两位同学的平均分都是95分,甲的成绩的方差是0.3,乙的成绩的方差是0.7,根据以上数据,下列说法正确的是( )
| A. | 甲的成绩比乙的成绩稳定 | B. | 乙的成绩比甲的成绩稳定 | ||
| C. | 甲、乙两人的成绩一样稳定 | D. | 无法确定甲、乙的成绩谁更稳定 |
 如图,某仓储中心有一斜坡AB,其坡度为i=1:2,顶部A处的高AC为4m,B、C在同一水平地面上.
如图,某仓储中心有一斜坡AB,其坡度为i=1:2,顶部A处的高AC为4m,B、C在同一水平地面上.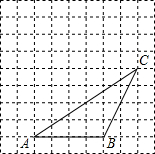 如图,△ABC的顶点都在方格纸的格点上.将△ABC向左平移2格,再向上平移4格.请在图中画出平移后的三角形A′B′C′,再在图中画出三角形A′B′C′的高C′D′.
如图,△ABC的顶点都在方格纸的格点上.将△ABC向左平移2格,再向上平移4格.请在图中画出平移后的三角形A′B′C′,再在图中画出三角形A′B′C′的高C′D′.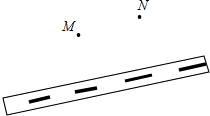 如图,靠近公路有两个村庄M、N,现在M村决定修建两条公路,一条与N村相连,一条与公路相连,请用图示说明这两条公路如何修建,使得费用最少(公路越短,费用越低,反之越高)并用你所学的数学知识作出图形(不必说明理由).
如图,靠近公路有两个村庄M、N,现在M村决定修建两条公路,一条与N村相连,一条与公路相连,请用图示说明这两条公路如何修建,使得费用最少(公路越短,费用越低,反之越高)并用你所学的数学知识作出图形(不必说明理由).