题目内容
16.甲、乙两家电器商场以相同价格试销同一种品牌电视机.在10天中,两家商场的日销售量分别统计如表:(单位:台)| 甲商场销量 | 1 | 3 | 2 | 3 | 0 | 1 | 2 | 3 | 1 | 4 |
| 乙商场销量 | 4 | 0 | 3 | 0 | 3 | 3 | 2 | 2 | 0 | 3 |
(2)甲、乙两家商场每天销售的中位数分别是多少?
(3)在10天中,哪家商场的销售量更稳定?为什么?
分析 (1)分别利用平均数的计算公式即可求得甲、乙两家商场的日平均销量;
(2)排序后计算位于中间两个数的平均数就是中位数;
(3)利用方差公式求得方差即可根据方差的大小确定哪家商场的销售量更稳定.
解答 解:(1)甲商场的日平均销量为:$\frac{1}{10}$(0+1×3+2×2+3×3+4)=2;
乙商场的日平均销量为:$\frac{1}{10}$(0×3+2×2+3×4+4)=2;
(2)把甲商场的日平均销量从小到大排列为:0,1,1,1,2,2,3,3,3,4,最中间两个数的平均数是(2+2)÷2=2(台),
则中位数是2台;
把乙商场的日平均销量从小到大排列为:0,0,0,2,2,3,3,3,3,4,最中间两个数的平均数是(2+3)÷2=2.5(台),
则中位数是2.5台;
(3)甲商场的销售量更稳定.
甲商场的日销售量的方差为$\frac{1}{10}$[(0-2)2+3×(1-2)2+2×(2-2)2+3×(3-2)2+(4-2)2]=1.4,
乙商场的日销售量的方差为$\frac{1}{10}$[3×(0-2)2+2×(2-2)2+4×(3-2)2+(4-2)2]=2;
∵1.4<2,
∴甲商场的销售量更稳定.
点评 本题考查方差、中位数和平均数,中位数是将一组数据从小到大(或从大到小)重新排列后,最中间的那个数(或最中间两个数的平均数);平均数是所有数据的和除以数据的个数;一般地设n个数据,x1,x2,…xn的平均数为$\overline{x}$,则方差S2=$\frac{1}{n}$[(x1-$\overline{x}$)2+(x2-$\overline{x}$)2+…+(xn-$\overline{x}$)2],它反映了一组数据的波动大小,方差越大,波动性越大,反之也成立.

| 甲队 | 7 | 8 | 9 | 7 | 10 | 10 | 9 | 10 | 10 | 10 |
| 乙队 | 10 | 8 | 7 | 9 | 8 | 10 | 10 | 9 | 10 | 9 |
(2)计算乙队的平均成绩和方差;
(3)已知甲队成绩的方差是1.4分2,则成绩较为整齐的是哪个队?
| A. | 直线a向上平移1个单位得到直线b | B. | 直线a向下平移1个单位得到直线b | ||
| C. | 直线a向左平移1个单位得到直线b | D. | 直线a向右平移1个单位得到直线b |
| A. | a-5>b-5 | B. | 2a>2b | C. | a-b>0 | D. | ac>bc |
 春耕期间,某农资门市部连续5填调进一批化肥销售.在开始调进化肥的第4天开始销售.若进货期间每天调入化肥的吨数与销售期间每天销售化肥的吨数都保持不变,这个门市部的化肥存量S(单位:t)与时间t(单位:天)之间的函数关系如图所示,则该门市部这次化肥销售活动(从开始进货到销售完毕)所用时间是7天.
春耕期间,某农资门市部连续5填调进一批化肥销售.在开始调进化肥的第4天开始销售.若进货期间每天调入化肥的吨数与销售期间每天销售化肥的吨数都保持不变,这个门市部的化肥存量S(单位:t)与时间t(单位:天)之间的函数关系如图所示,则该门市部这次化肥销售活动(从开始进货到销售完毕)所用时间是7天.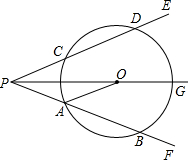 如图,射线PG平分∠EPF,O为射线PG上一点,以O为圆心,10为半径作⊙O,分别与∠EPF两边相交于A、B和C、D,连结OA,此时有OA∥PE
如图,射线PG平分∠EPF,O为射线PG上一点,以O为圆心,10为半径作⊙O,分别与∠EPF两边相交于A、B和C、D,连结OA,此时有OA∥PE 在△ABC中,∠A=$\frac{1}{2}$∠B=∠ACB+20°,CD为∠ACB的平分线,求∠A及∠BDC的度数.
在△ABC中,∠A=$\frac{1}{2}$∠B=∠ACB+20°,CD为∠ACB的平分线,求∠A及∠BDC的度数.