题目内容
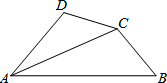 如图,在四边形ABCD中,给出下列三个论断:
如图,在四边形ABCD中,给出下列三个论断:①对角线AC平分∠BAD;
②CD=BC;
③∠D+∠B=180°.
在上述三个论断中,若以其中两个论断作为条件,另外一个论断作结论,则可以得出
考点:全等三角形的判定与性质,角平分线的性质
专题:
分析:过点C作CE⊥AB,CF⊥AD,垂足为E、F,①②作为条件,可以证明△CBE与△CDF全等,根据全等三角形对应角相等可得∠B=∠CDF,再根据平角定义得到∠B+∠D=180°,所以③作为结论是正确的命题;①③作为条件,与前一种情况的思路相反,可以根据条件证明△CBE与△CDF全等,再根据全等三角形对应边相等得到CD=BC,所以②作为结论是正确的命题;②③作为条件,先证明∠B=∠CDF,再根据“角角边”证明△CBE与△CDF全等,根据全等三角形对应边相等可得CE=CF,再根据到角的两边距离相等的点在角的平分线上可得AC平分∠BAD,所以①作为结论是正确命题;
解答:解:(1)共有:①②作为条件,③作为结论,
①③作为条件,②作为结论,
②③作为条件,①作为结论,3种情况,都是真命题,
故可以写出3个正确的命题;
故答案为3.
①③作为条件,②作为结论,
②③作为条件,①作为结论,3种情况,都是真命题,
故可以写出3个正确的命题;
故答案为3.
点评:本题考查了全等三角形的判定与性质,以及条件的排列与组合,作出辅助线构造出全等三角形是解题的关键,是开放型题目,答案不唯一.

练习册系列答案
 小题狂做系列答案
小题狂做系列答案
相关题目
将二次函数y=2x2-8x-1化成y=a(x-h)2+k的形式,结果为( )
| A、y=2(x-2)2-1 |
| B、y=2(x-4)2+32 |
| C、y=2(x-2)2-9 |
| D、y=2(x-4)2-33 |
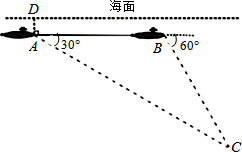 如图,一艘核潜艇在海面下500米A处测得俯角为30°正前方的海底C处有黑匣子信号发出,继续在同一深度直线航行4000米后在B处测得俯角为60°正前方的海底C处有黑匣子信号发出.点C和直线AB在同一铅垂面上,求点C距离海面的深度(结果保留根号).
如图,一艘核潜艇在海面下500米A处测得俯角为30°正前方的海底C处有黑匣子信号发出,继续在同一深度直线航行4000米后在B处测得俯角为60°正前方的海底C处有黑匣子信号发出.点C和直线AB在同一铅垂面上,求点C距离海面的深度(结果保留根号). 如图,直线l:y=
如图,直线l:y= 如图所示的图案是一个轴对称图形,若将其中的任意一个白色方块涂黑,所得的图案仍为轴对称图形的概率为
如图所示的图案是一个轴对称图形,若将其中的任意一个白色方块涂黑,所得的图案仍为轴对称图形的概率为 如图,点B是半径为6的⊙O上一点,过点B作一个30°的圆周角∠ABC,则由弦AB、BC和
如图,点B是半径为6的⊙O上一点,过点B作一个30°的圆周角∠ABC,则由弦AB、BC和